题目内容
7.阅读下面的问题:$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}-1$;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}-\sqrt{2}$;
$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$
…
(1)求$\frac{1}{\sqrt{8}+\sqrt{7}}$的值;
(2)已知m是正整数,求$\frac{1}{\sqrt{m+1}-\sqrt{m}}$的值;
(3)计算$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$…+$\frac{1}{\sqrt{2015}+\sqrt{2014}}$+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$.
分析 (1)由规律可得,$\frac{1}{\sqrt{8}+\sqrt{7}}$=2$\sqrt{2}$-$\sqrt{7}$;
(2)利用分母有理化化简,可得结果;
(3)先利用分母有理化化简,再计算可得结果.
解答 解:(1)$\frac{1}{\sqrt{8}+\sqrt{7}}$=$\frac{\sqrt{8}-\sqrt{7}}{(\sqrt{8}+\sqrt{7})(\sqrt{8}-\sqrt{7})}$=2$\sqrt{2}$-$\sqrt{7}$;
(2)原式=$\frac{\sqrt{m+1}+\sqrt{m}}{(\sqrt{m+1}-\sqrt{m})(\sqrt{m+1}+\sqrt{m})}$=$\sqrt{m+1}+\sqrt{m}$;
(3)原式=$\sqrt{2}$-1+$\sqrt{3}$$-\sqrt{2}$+2$-\sqrt{3}$+…+$\sqrt{2015}$$-\sqrt{2014}$+$\sqrt{2016}$-$\sqrt{2015}$,
=$\sqrt{2016}-1$,
=12$\sqrt{14}$-1.
点评 本题主要考查了利用分母有理化,利用平方差公式,找出有理化因式是解答此题的关键.

练习册系列答案
相关题目
17.a<b,则下列不等式一定成立的是( )
| A. | a2<b2 | B. | ac2<bc2 | C. | ac<bc | D. | a-b<0 |
15.若y轴上的点A到x轴的距离为3,则点A的坐标为( )
| A. | (3,0) | B. | (3,0)或(-3,0) | C. | (0,3) | D. | (0,3)或(0,-3) |
2. 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
17.-$\frac{1}{2}$的绝对值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
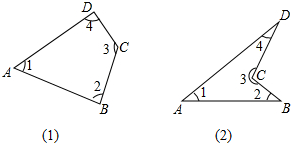 求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.
求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.