题目内容
14.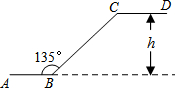 如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.
如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是$6\sqrt{2}$m,则乘电梯从点B到点C上升的高度h是6m.
分析 作CF⊥AB的延长线于F,求出∠CBF=45°,然后利用三角函数求出CF的长即可.
解答  解:作CF⊥AB的延长线于F,∵∠ABC=135°,
解:作CF⊥AB的延长线于F,∵∠ABC=135°,
∴∠CBF=180°-135°=45°,
∴CF=BC•sin45°=6$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=6.
故答案为6.
点评 本题考查了解直角三角形的应用--坡度坡角问题,熟悉三角函数是解题的关键.

练习册系列答案
相关题目
2. 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
9. 如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )
如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )
 如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )
如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )| A. | 16 | B. | 20 | C. | 12 | D. | 24 |
3.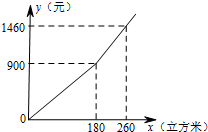 为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )
为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )
 为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )
为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )| A. | 240立方米 | B. | 236立方米 | C. | 220立方米 | D. | 200立方米 |
 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.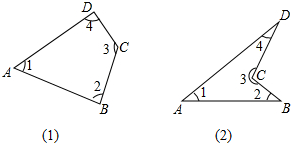 求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数.
求图(1)和图(2)中的∠1+∠2+∠3+∠4的度数. 如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD.若∠EAO=15°,求∠BOE的度数.
如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD.若∠EAO=15°,求∠BOE的度数.