题目内容
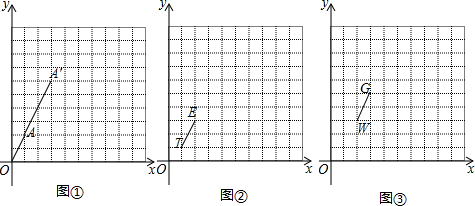
13.解决下面问题:(1)阅读理解:如图①,在平面直角坐标系中,点A坐标为(1,2)连接OA并延长OA至A′,使OA′:OA=3:1,则点A′的坐标为(3,6);
(2)活动探索:(在下图中分别作出对应的图形,不要求用尺规作图)
活动一:如图②,在平面直角坐标系中,点T(1,1)、点E(2,3),连接TE并延TE长至点E′,使T E′:TE=3:1,则点E′的坐标为(4,7);
活动二:如图③,在平面直角坐标系中,点W(2,3)、点G(3,5),连接WG并延长WG至点G′,使WG′:WG=4:1,则点G′的坐标为(6,11);
(3)归纳猜想:
在平面直角坐标系中,若点M(a,b)、点P(x,y),连接MP并延长MP至点P′,使MP′:MP=n:1,则点P′的横坐标为nx-na+a,纵坐标为ny-nb+b.(用a,b,x,y,n表示,其中0<a<x,0<b<y,n为大于1的正整数)
分析 根据第一问给出的信息,我们很容易对第二问和第三问进行解答,第二问根据题目中的信息作出相应的图形,从而可以写出E′和G′的坐标;根据第二问对第三问进行猜想,得出P′的坐标.
解答 解:根据第一问可得,
(2)活动一中,点E′的坐标为(4,7),如下图所示:
∵在平面直角坐标系中,点T(1,1)、点E(2,3),T E′:TE=3:1,
设E′的坐标为(x,y).
∴$\frac{x-1}{2-1}=\frac{3}{1},\frac{y-1}{3-1}=\frac{3}{1}$.
解得,x=4,y=7.
故点E的坐标为(4,7).
活动二中,点G′的坐标为(6,11),如下图所示:
∵在平面直角坐标系中,点W(2,3)、点G(3,5),WG′:WG=4:1,
设点G′的坐标为(x,y).
∴$\frac{x-2}{3-2}=\frac{4}{1},\frac{y-3}{5-3}=\frac{4}{1}$.
解得,x=6,y=11
∴点G′的坐标为(6,11).
(3)∵在平面直角坐标系中,点M(a,b)、点P(x,y),MP′:MP=n:1,其中0<a<x,0<b<y,
设点P′的坐标为(h,k).
∴$\frac{h-a}{x-a}=\frac{n}{1},\frac{k-b}{y-b}=\frac{n}{1}$.
解得,h=nx-na+a,k=ny-nb+b
点评 本题考查坐标和图形的相关知识,关键是明确图形变化之后对应边的比,根据对应边的比相等,求出相应的点的坐标.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
1.天王星早晨的气温为-30℃,中午上升了70℃,半夜又下降了80℃,则半夜的气温是( )
| A. | 40℃ | B. | -40℃ | C. | -50℃ | D. | -180℃ |
3. 表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )
表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )
 表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )
表示a,b两数的点在数轴上位置如图所示,则下列判断错误的是( )| A. | a+b<0 | B. | a-b<0 | C. | a×b>0 | D. | |a|>b |
 如图,已知△ABC和△ABD,∠CAB=∠DBA=90°,BC=5,BD=8,∠CBD=2∠ADB,则AD的长为4$\sqrt{5}$.
如图,已知△ABC和△ABD,∠CAB=∠DBA=90°,BC=5,BD=8,∠CBD=2∠ADB,则AD的长为4$\sqrt{5}$. 如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,垂足为E,AD平分∠BAC.
如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,垂足为E,AD平分∠BAC.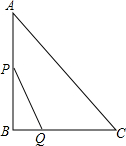 如图,Rt△ABC中∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x秒.
如图,Rt△ABC中∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x秒.