题目内容
4.一元二次方程a(x-1)2+b(x-1)+c=0化为一般形式后为2x2-3x-1=0,试求a,b,c的值.分析 根据一元二次方程的一般形式,可得方程组,根据解方程组,可得答案.
解答 解:一元二次方程a(x-1)2+b(x-1)+c=0化为一般形式后为ax2-(2a-b)x-(b-a-c)=0,
一元二次方程a(x-1)2+b(x-1)+c=0化为一般形式后为2x2-3x-1=0,得
$\left\{\begin{array}{l}{a=2}\\{2a-b=3}\\{b-a-c=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=1}\\{c=-2}\end{array}\right.$.
点评 本题考查了一元二次方程的一般形式,利用一元二次方程的一般形式得出方程组是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.直角坐标系,正方形ABCD的两个顶点坐标为A(-1,0)、C(-1,4),点D在第二象限,则点B的坐标为( )
| A. | (-3,2) | B. | (-1,2) | C. | (1,2) | D. | (1,1) |
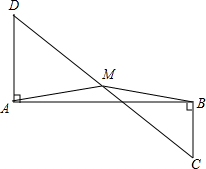 已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.
已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.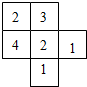 如图所示是由几个小立方体所组成几何体的从上面看到的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体从正面、从左面看到的形状图.
如图所示是由几个小立方体所组成几何体的从上面看到的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体从正面、从左面看到的形状图.