题目内容
2.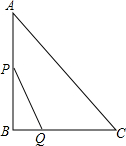 如图,Rt△ABC中∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x秒.
如图,Rt△ABC中∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x秒.(1)用含x的代数式表示BQ为xcm,PB为8-2xcm;
(2)是否存在x的值,使得四边形APQC的面积等于20cm2?若存在,请求出此时x的值;若不存在,请说明理由.
分析 (1)首先运用勾股定理求出AB边的长度,然后根据路程=速度×时间,分别表示出BQ、PB的长度;
(2)根据四边形APQC的面积=△ABC的面积-△PBQ的面积,列出方程,根据解的情况即可判断.
解答 解:(1)∵∠B=90°,AC=10,BC=6,
∴AB=8.
∴BQ=x,PB=8-2x;
(2)假设存在x的值,使得四边形APQC的面积等于20cm2,
则$\frac{1}{2}$×6×8-$\frac{1}{2}$x(8-2x)=20,
解得:x1=x2=2.
假设成立,所以当x=2时,四边形APQC面积的面积等于20cm2.
点评 此题考查一元二次方程的实际运用,三角形的面积,利用三角形的面积差建立方程是解决问题的关键.

练习册系列答案
相关题目
11.在有理数|-8|,-|-8|,-(-8),-82,m2中,非负数有( )个.
| A. | 一个 | B. | 2个 | C. | 3个 | D. | 4个 |
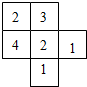 如图所示是由几个小立方体所组成几何体的从上面看到的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体从正面、从左面看到的形状图.
如图所示是由几个小立方体所组成几何体的从上面看到的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体从正面、从左面看到的形状图.