题目内容
3. 如图,已知△ABC和△ABD,∠CAB=∠DBA=90°,BC=5,BD=8,∠CBD=2∠ADB,则AD的长为4$\sqrt{5}$.
如图,已知△ABC和△ABD,∠CAB=∠DBA=90°,BC=5,BD=8,∠CBD=2∠ADB,则AD的长为4$\sqrt{5}$.
分析 在BD上E,截取BE=AC,证得△ABE≌△BAC,得出AE=BC=5,∠AEB=∠ACB,再利用AC∥BD和∠CBD=2∠ADB证得DE=AE=5,求得BE.进一步利用勾股定理解决问题.
解答 解:如图,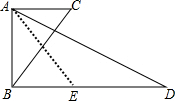
在BD上E,截取BE=AC,
∵在△ABE和△BAC中,
$\left\{\begin{array}{l}{AB=BA}\\{∠ABE=∠BAC=90°}\\{BE=AC}\end{array}\right.$,
∴△ABE≌△BAC,
∴AE=BC=5,∠AEB=∠ACB,
∵∠CAB=∠DBA=90°,
∴AC∥BD,
∴∠ACB=∠CBD,
∴∠AEB=∠CBD,
∵∠CBD=2∠ADB,
∴∠AEB=2∠ADB=∠ADB+∠DAE,
∴∠DAE=∠ADB,
∴EA=ED=5,
∴BE=BD-DE=8-5=3,
∴AB=$\sqrt{A{E}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$.
故答案为:4$\sqrt{5}$.
点评 此题考查三角形全等的判定与性质,勾股定理的运用,平行线的判定与性质,正确作出辅助线,构造三角形全等是解决问题的关键.

练习册系列答案
相关题目
13.根据关于x的一元二次方程x2+px+q=1,可列表如下:则方程x2+px+q=1的正数解满足( )
| x | 0 | 0.5 | 1 | 1.1 | 1.2 | 1.3 |
| x2+px+q | -15 | -8.75 | -2 | -0.59 | 0.84 | 2.29 |
| A. | 0.5<x<1 | B. | 1<x<1.1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
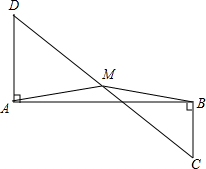 已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.
已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.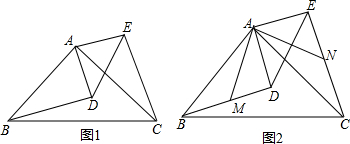
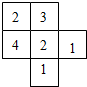 如图所示是由几个小立方体所组成几何体的从上面看到的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体从正面、从左面看到的形状图.
如图所示是由几个小立方体所组成几何体的从上面看到的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体从正面、从左面看到的形状图.