题目内容

如图，在正△ABC中，D，E分别在AC，AB上，且，AE＝BE，则有

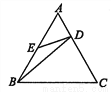
A. △AED∽△ABC B. △ADB∽△BED

C. △BCD∽△ABC D. △AED∽△CBD

D 【解析】试题分析：因为△ABC是正三角形，所以∠A＝∠C＝60°，可设AD＝a，则AC＝3a，而AB＝AC＝BC＝3a，所以AE＝BE＝a，所以＝＝，又＝＝，所以＝，∠A＝∠C＝60°，故△AED∽△CBD，故选：D．
练习册系列答案
相关题目

计算：

（1）|﹣5|+﹣32

（2）|﹣2|﹣（﹣1）+．

（1）原式=0；（2）原式=﹣1﹣2． 【解析】试题分析：（1）根据绝对值的性质、平方根的定义及乘方的运算法则分别计算各项后，再合并即可；（2）根据绝对值的性质、去括号法则及立方根的定义分别计算各项后，再合并即可. 试题解析： （1）原式=5+4﹣9=0； （2）原式=2﹣﹣+1﹣4=﹣1﹣2．

如图，OP平分∠AOB，PA⊥OA,PB⊥OB，垂足分别为A，B。下列结论中不一定成立的是（ ）

A、PA=PB B、PO平分∠AOB

C、OA=OB D、AB垂直平分OP

D 【解析】 试题分析：本题要从已知条件OP平分∠AOB入手，利用角平分线的性质：因OP平分∠AOB，PA⊥OA，PB⊥OB，得到PA=PB，进而推出△AOE≌△BOE，从未得到∠APO=∠BPO，OA=OB，因此A、B、C项正确；设PO与AB相交于E，由OA=OB，∠AOP=∠BOP，OE=OE，得证△AOE≌△BOE，进而得∠AEO=∠BEO=90°，因此得证OP垂直AB，而不能得...

如果2+是方程的一个根，那么的值是__________.

4 【解析】试题解析：把2+代入方程中可得（2+）2-c（2+）+1=0， 解得c=4．

如图，在△ABC中，∠ABC=90°，DE垂直平分AC，垂足为O，AD∥BC，且AB=3，BC=4，则AD的长为

A. B. C. D.

B 【解析】试题解析：∵Rt△ABC中，∠ABC=90°，AB=3，BC=4， ∴AC==5， ∵DE垂直平分AC，垂足为O， ∴OA=AC=，∠AOD=∠B=90°， ∵AD∥BC， ∴∠A=∠C， ∴△AOD∽△CBA， ∴， 即， 解得AD=. 故选B．

方程x2+2x-5=0经过配方后，其结果正确的是

A. B.

C. D.

C 【解析】试题分析：根据配方法的意义，可知在方程的两边同时加减一次项系数的一半的平方，可知，即，配方为. 故选：C.

A、B两站相距960公里，一列慢车从A站开出，每小时行驶120公里，一列快车从B站开出，每小时行驶200公里.慢车先行1小时，快车再开，两车相向而行，慢车多少小时后两车相距200公里？

慢车3小时或小时后两车相距200公里. 【解析】试题分析：设慢车开出x小时后两车相距200公里，有两种情况，一种是两车相遇前相距200公里，一种是两车相遇后又相距200公里，根据等量关系：两车的路程和=总路程，列方程进行求解即可. 试题解析：设慢车开出x小时后两车相距200公里，则： （1）当两车未相遇时，相距200公里，方程为： 120x+200（x-1）+200=960...

整式-0.3x2y，0， ， ， ， 中，单项式的个数有（　　）

A. 3个 B. 4个 C. 5个 D. 6个

B 【解析】-0.3x2y是单项式；0是单项式； 是多项式； 是单项式； 是单项式； 是多项式，单项式共有4个， 故选B.

规定用符号[m]表示一个实数m的整数部分，例如：[]=0，[3.14]=3．按此规定[]的值为_____．

4 【解析】∵3< <4，∴4< +1<5，∴[]=4.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网