题目内容
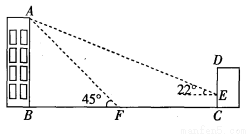
(本题满分8分)如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求教学楼AB的高度.
(参考数据:sin22°≈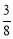 ,cos22°≈
,cos22°≈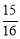 ,tan22°≈
,tan22°≈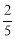 )
)
12
【解析】
试题分析:过点E作EM⊥AB,垂足为M. 然后解Rt△ABF和Rt△AEM即可.
试题解析:过点E作EM⊥AB,垂足为M.

设AB为x.在Rt△ABF中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13,
在Rt△AEM中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,
又∵ ,∴
,∴ ,解得:x≈12.
,解得:x≈12.
答:教学楼AB的高为12m.
考点:解直角三角形的应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 +2y的值是3,则多项式
+2y的值是3,则多项式 (
( )与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,
)与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2, .
.
 ,下面给出的说法不正确的是( ).
,下面给出的说法不正确的是( ). 的解相同
的解相同  ,得
,得 ,可以解得
,可以解得
 ,可以解得
,可以解得 .
.


 ) C.(0,
) C.(0, ) D.(0,
) D.(0, )
)
 中,∠MAN=45°,∠MAN绕点
中,∠MAN=45°,∠MAN绕点 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交 (或它们的延长线)于点
(或它们的延长线)于点 .
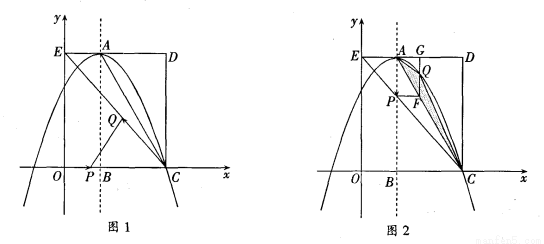
. 旋转到BM=DN时(如图1),易证BM+DN=MN.
旋转到BM=DN时(如图1),易证BM+DN=MN.
 旋转到BM≠DN时(如图2),线段
旋转到BM≠DN时(如图2),线段 和
和 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明. 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段 和
和 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.