题目内容
如图,AB是⊙O的直径,AM、BN分别切⊙O于点A、B,CD交AM,BN于点D、C,DO平分∠ADC.

(1)求证:CD是⊙O的切线;
(2)若AD=4,BC=9,求⊙O的半径R.
(1)见解析;(2)过点D作DF⊥BC于点F,将梯形ABCD分割成一个矩形和一个直角三角形,得出FC=9﹣4=5,根据切线长定理得DC=AD+BC=4+9=13,然后在直角三角形DCF中用勾股定理求出DF的长,可解.
【解析】
试题分析:(1)过点O作OE⊥DC于E,然后利用角平分线的性质证明OE=OA即可;(2)
试题解析:(1)证明:过O点作OE⊥CD于点E,
∵AM切⊙O于点A,
∴OA⊥AD,
又∵DO平分∠ADC,
∴OE=OA,
∵OA为⊙O的半径,
∴CD是⊙O的切线. 3分
(2)【解析】
过点D作DF⊥BC于点F,

∴AM,BN分别切⊙O于点A,B,
∴AB⊥AD,AB⊥BC,
∴四边形ABFD是矩形,
∴AD=BF,AB=DF,
又∵AD=4,BC=9,
∴FC=9﹣4=5,
∴AM,BN,DC分别切⊙O于点A,B,E,
∴DA=DE,CB=CE,
∴DC=AD+BC=4+9=13, 6分
在RT△DFC中, DC2=DF2+FC2,
∴DF= =12,
=12,
∴AB=12,
∴⊙O的半径R是6. 8分
考点:1.切线的判定;2.矩形的性质;3.切线长定理;4.勾股定理.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 = .
= .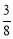 ,cos22°≈
,cos22°≈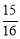 ,tan22°≈
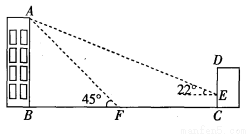
,tan22°≈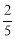 )
)
 (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。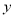 =f(x)=
=f(x)=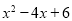 的图象向左平移1个单位,再向上平移1个单位,所得图象对
的图象向左平移1个单位,再向上平移1个单位,所得图象对

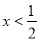 时,y随x的增大而减小
时,y随x的增大而减小