题目内容
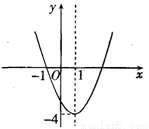
如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )

A.(0,2) B.(0, ) C.(0,
) C.(0, ) D.(0,
) D.(0, )
)
A
【解析】
试题分析:因为抛物线y=-x2+px+q的对称轴为直线x=-3,过点N(-1,1),所以 ,解得
,解得 ,所以
,所以 ,所以顶点M为(-3,5),则点M关于y轴的对称点
,所以顶点M为(-3,5),则点M关于y轴的对称点 为(3,5),设直线
为(3,5),设直线 N的解析式为
N的解析式为 ,把点N(-1,1),点
,把点N(-1,1),点 (3,5),代入得
(3,5),代入得 ,解得
,解得 ,所以直线为
,所以直线为 ,令x=0,则y=2,所以点P的坐标为(0,2),故选:A.
,令x=0,则y=2,所以点P的坐标为(0,2),故选:A.
考点:1.待定系数法求函数解析式;2.轴对称;3.直线与y的交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.1.31×
B.1.31× C.1.31×
C.1.31× D.0.131×
D.0.131×
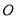 为投影中心,长度为1的线段
为投影中心,长度为1的线段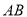 平行于它在面
平行于它在面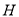 内的投影
内的投影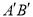 ,投影
,投影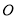 到直线
到直线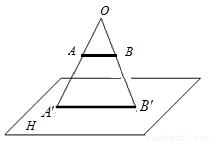
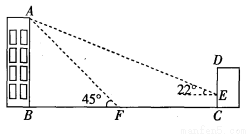
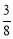 ,cos22°≈
,cos22°≈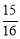 ,tan22°≈
,tan22°≈ )
)
 (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数)。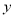 =f(x)=
=f(x)=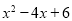 的图象向左平移1个单位,再向上平移1个单位,所得图象对
的图象向左平移1个单位,再向上平移1个单位,所得图象对