题目内容
(本题满分13分)如图,抛物线 (
( )与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,
)与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2, .
.

(1)求点A、B、E的坐标;
(2)求抛物线的解析式;
(3)在第一象限的抛物线上,是否存在一点M,作MN⊥x轴,垂足为N,使得以M、N、O为顶点的三角形与△AOC相似.
(1)点B、E的坐标为(3,0)(-1,0);(2) ;(3)点M
;(3)点M 和
和 .
.
【解析】
试题分析:(1)证明△ ∽△
∽△ ,然后利用相似三角形的性质求出线段OA、OE、OB的长即可;(2)将点C、B、E的坐标分别代入
,然后利用相似三角形的性质求出线段OA、OE、OB的长即可;(2)将点C、B、E的坐标分别代入 ,然后解方程组即可;(3)假设存在点M的坐标为
,然后解方程组即可;(3)假设存在点M的坐标为 ,N的坐标为
,N的坐标为 适合题意,然后分△
适合题意,然后分△ ∽△
∽△ 或△
或△ ∽△
∽△ 两种情况讨论即可.
两种情况讨论即可.
试题解析:【解析】
(1)因为 ,
,
所以 ,
, .
.
所以 .
.
所以△ ∽△
∽△ .
.
所以 ·
·
又因为点C、D的坐标分别为(0,2),(-4,0)
所以 ,所以点A的坐标为(1,0)
,所以点A的坐标为(1,0)
因为AB= AE=2,所以点B、E的坐标为(3,0)(-1,0);
(2)因为抛物线经过C、B、E,所以将(0,2)(3,0)(-1,0)代入 得:
得:
 ,解得:
,解得: ,
, ,
, .
.
所以抛物线解析式为: .
.
(3)假设存在点M的坐标为 ,N的坐标为
,N的坐标为 适合题意,
适合题意,
①若△ ∽△
∽△ ,因为
,因为
则 即
即
所以 ,解得
,解得 或
或 (舍去)
(舍去)
②若△ ∽△
∽△ ,因为
,因为
则 即
即
所以 ,解得
,解得 或
或 (舍去)
(舍去)
综上可知存在点M 和
和 得以M、N、O为顶点的三角形与△AOC相似···13分
得以M、N、O为顶点的三角形与△AOC相似···13分
考点:1.相似三角形的判定与性质;2.待定系数法求函数解析式;3.函数与几何知识的综合.

练习册系列答案
相关题目
 .
. B.1.31×
B.1.31× C.1.31×
C.1.31× D.0.131×
D.0.131×
 = .
= .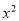 +mx-n,则
+mx-n,则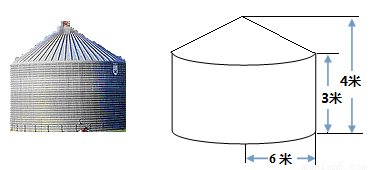
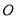 为投影中心,长度为1的线段
为投影中心,长度为1的线段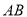 平行于它在面
平行于它在面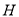 内的投影
内的投影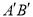 ,投影
,投影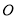 到直线
到直线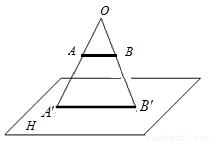
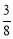 ,cos22°≈
,cos22°≈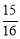 ,tan22°≈
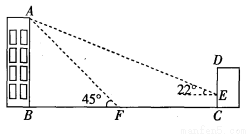
,tan22°≈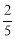 )
)
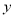 =f(x)=
=f(x)=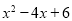 的图象向左平移1个单位,再向上平移1个单位,所得图象对
的图象向左平移1个单位,再向上平移1个单位,所得图象对