��Ŀ����
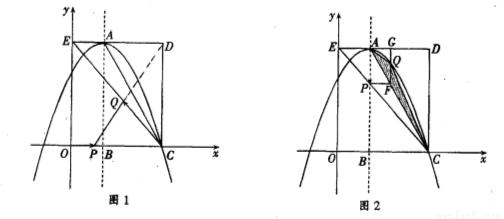
����������12�֣���ͼ����ƽ��ֱ������ϵ�У�����OCDE����������ֱ���C��3��0����D��3��4����E��0��4������A��DE�ϣ���AΪ����������߹���C���ҶԳ���x=1��x���ڵ�B������EC��AC����P��QΪ���㣬���˶�ʱ��Ϊt�룮
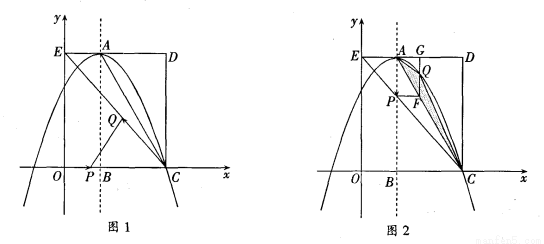
��1����գ���A����Ϊ �������ߵĽ���ʽΪ ��
��2����ͼ1�У�����P���߶�OC�ϴӵ�O���C��1����λ������ٶ��˶���ͬʱ����Q���߶�CE�ϴӵ�C��E��2����λ������ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�������PQ���Ƿ����ʵ��t��ʹ��PQ���ڵ�ֱ�߾�����D�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
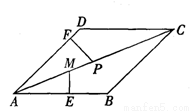
��3����ͼ2�У�����P�ڶԳ����ϴӵ�A��ʼ���B��1����λ������ٶ��˶�������P��PF��AB����AC�ڵ�F������F��FG��AD�ڵ�G�����������ڵ�Q������AQ��CQ����tΪ��ֵʱ����ACQ�����������ֵ�Ƕ��٣�
��1����A����Ϊ��1��4����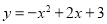 ����2����t=1��s��ʱ��PQ���ڵ�ֱ�߾�����D����3����t=2ʱ����ACQ�����������ֵ��1��
����2����t=1��s��ʱ��PQ���ڵ�ֱ�߾�����D����3����t=2ʱ����ACQ�����������ֵ��1��
��������
�����������1�����þ���OCDE����������ֱ���C��3��0����D��3��4����E��0��4���ͶԳ���x=1�ɵõ�A�����꣨1��4�����������ߵĽ���ʽΪ ��C��3��0�����������ߵĽ���ʽ���ɵ�a= -1����2����PQ���ڵ�ֱ�߾�����D����ΪDE//CP�����ԡ�DEQ�ס�PCQ���Ӷ��ɵ�
��C��3��0�����������ߵĽ���ʽ���ɵ�a= -1����2����PQ���ڵ�ֱ�߾�����D����ΪDE//CP�����ԡ�DEQ�ס�PCQ���Ӷ��ɵ�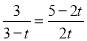 ���ⷽ�̼��ɣ�3�������ֱ��AC�Ľ���ʽy=��2x+6����P��1��4��t��������ɱ�ʾ����Q�����꣬�ú���t�Ĵ���ʽ��ʾ��S��ACQ=S��AFQ+S��CPQ��Ȼ����ݶ��κ��������ʽ�ɣ�
���ⷽ�̼��ɣ�3�������ֱ��AC�Ľ���ʽy=��2x+6����P��1��4��t��������ɱ�ʾ����Q�����꣬�ú���t�Ĵ���ʽ��ʾ��S��ACQ=S��AFQ+S��CPQ��Ȼ����ݶ��κ��������ʽ�ɣ�
�����������������
��1���������ߵĶԳ���Ϊx=1������OCDE����������ֱ���C��3��0����D��3��4����E��0��4������A��DE�ϣ����A����Ϊ��1��4�����������ߵĽ���ʽΪ ��C��3��0�����������ߵĽ���ʽ���ɵ�
��C��3��0�����������ߵĽ���ʽ���ɵ�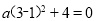 �����a=��1���������ߵĽ���ʽΪ
�����a=��1���������ߵĽ���ʽΪ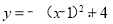
��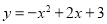 ��
��
��2����PQ���ڵ�ֱ�߾�����D����ΪDE//CP�����ԡ�DEQ�ס�PCQ������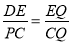 ,
,
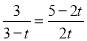 ��
��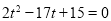 �����
�����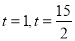 ����ȥ������t=1��s��ʱ��PQ���ڵ�ֱ�߾�����D��
����ȥ������t=1��s��ʱ��PQ���ڵ�ֱ�߾�����D��
��3����ֱ��AC�Ľ���ʽΪy=kx+b����A��1��4����C��3��0������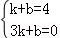 �����
�����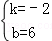 ��
��
��ֱ��AC�Ľ���ʽΪy=��2x+6��
��P��1��4��t������y=4��t����y=��2x+6�У���x=1+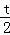 ����Q��ĺ�����Ϊ1+
����Q��ĺ�����Ϊ1+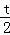 ��
��
��x=1+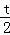 ����
����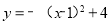 ����y=4��
����y=4��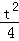 ��
��
��Q���������Ϊ4��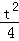 ����QF=��4��
����QF=��4��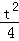 ������4��t��=t��
������4��t��=t��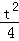 ��
��
��S��ACQ=S��AFQ+S��CPQ=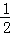 FQAG+
FQAG+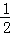 FQDG=
FQDG=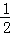 FQ��AG+DG��=
FQ��AG+DG��=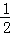 FQAD=
FQAD=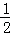 ��2��t��
��2��t��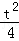 ��=
��= ��
��
�൱t=2ʱ����ACQ�����������ֵ��1��
���㣺1�����ε����ʣ�2������ϵ������3�����������ε��ж������ʣ�4�����κ��������ʣ�

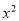 +mx��n����
+mx��n����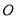 ΪͶӰ���ģ�����Ϊ1���߶�
ΪͶӰ���ģ�����Ϊ1���߶�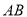 ƽ����������
ƽ����������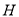 �ڵ�ͶӰ
�ڵ�ͶӰ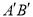 ��ͶӰ
��ͶӰ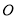 ��ֱ��
��ֱ��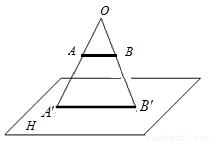
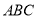 �͡�
�͡�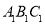 �У�����������������ĸ���Ϊ�� ����
�У�����������������ĸ���Ϊ�� ����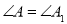 ��
��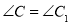 �����
�����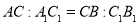 ��
��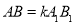 ��
��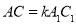 ��
��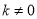 ����
����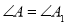 �����
�����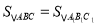 �����
�����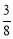 ��cos22���
��cos22���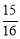 ��tan22���
��tan22���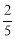 ��
��
 ��1��x��20����xΪ����������10������ۼ۸�Q2��Ԫ������������ʱ��x���죩֮�������¹�ϵ��Q2=45��21��x��30����xΪ��������
��1��x��20����xΪ����������10������ۼ۸�Q2��Ԫ������������ʱ��x���죩֮�������¹�ϵ��Q2=45��21��x��30����xΪ��������