题目内容
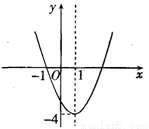
如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n= .

5
【解析】
试题分析:由题意可得:OA=4,AM=m,OC=4,CN=n,BN=4-n,BM=4-m,易证△OCN∽△NBM,所以 ,所以
,所以 ,所以
,所以 ,所以当n=2时,m的值最小为3,又在△OAM中,
,所以当n=2时,m的值最小为3,又在△OAM中, ,所以当m取最小值时,OM最小,所以m=3,n=2,所以m+n=5.
,所以当m取最小值时,OM最小,所以m=3,n=2,所以m+n=5.
考点:1.正方形的性质;2.相似三角形的判定与性质;3.二次函数的最值.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目



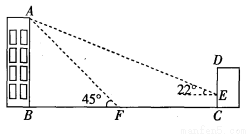
 ,cos22°≈
,cos22°≈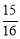 ,tan22°≈
,tan22°≈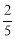 )
)
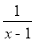 )÷
)÷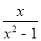 ,再选择一个恰当的x值代人并求值.
,再选择一个恰当的x值代人并求值.