题目内容
18. 如图,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值为( )
如图,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值为( )| A. | 2$\sqrt{3}$≤a≤4 | B. | a≤4 | C. | $\sqrt{3}$≤a≤2 | D. | a≥2$\sqrt{3}$ |
分析 根据题意,即是求该正六边形的边心距的2倍.构造一个由半径、半边、边心距组成的直角三角形,且其半边所对的角是30°,再根据锐角三角函数的知识求解.
解答 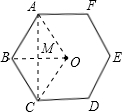 解:设正多边形的中心是O,其一边是AB,
解:设正多边形的中心是O,其一边是AB,
∴∠AOB=∠BOC=60°,
∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,
∵AB=2,∠AOB=60°,
∴cos∠BAC=$\frac{AM}{AB}$,
∴AM=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∵OA=OC,且∠AOB=∠BOC,
∴AM=MC=$\frac{1}{2}$AC,
∴AC=2AM=2$\sqrt{3}$.
∴a≥2$\sqrt{3}$.
故选D.
点评 本题考查了正多边形和圆,构造一个由半径、半边、边心距组成的直角三角形,运用锐角三角函数进行求解是解此题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
8. 如图,下列各点在阴影区域的是( )
如图,下列各点在阴影区域的是( )
 如图,下列各点在阴影区域的是( )
如图,下列各点在阴影区域的是( )| A. | (3,2) | B. | (-3,-2) | C. | (3,-2) | D. | (-3,2) |
9.下列关系式中,y是x的函数有( )
①y=$\frac{1}{2}x$;②y=x2;③y2=x(x≥0);④y=$\sqrt{x}$(x≥0);⑤y=±$\sqrt{x}$(x≥0);⑥|y|=x(x≥0);⑦y=|x|.
①y=$\frac{1}{2}x$;②y=x2;③y2=x(x≥0);④y=$\sqrt{x}$(x≥0);⑤y=±$\sqrt{x}$(x≥0);⑥|y|=x(x≥0);⑦y=|x|.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
3.下列数据是按一定规律排列的:
第一行:1
第二行:2 3
第三行:4 5 6
第四行:7 8 9 10
…
若正整数2016位于第a行,从左数第b个数,则a+b的值为( )
第一行:1
第二行:2 3
第三行:4 5 6
第四行:7 8 9 10
…
若正整数2016位于第a行,从左数第b个数,则a+b的值为( )
| A. | 53 | B. | 126 | C. | 2015 | D. | 1892 |
 如图,在△ABC中,AB=AC,∠BAC=α,BD⊥AC于D,CE⊥AB于E,BD与CE的交点为F,连接AF并延长交BC于G.
如图,在△ABC中,AB=AC,∠BAC=α,BD⊥AC于D,CE⊥AB于E,BD与CE的交点为F,连接AF并延长交BC于G.
 已知矩形ABCD,AB=6,AD=4$\sqrt{3}$
已知矩形ABCD,AB=6,AD=4$\sqrt{3}$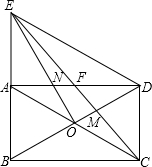 如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.
如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.