题目内容

15．一个多边形除去一个内角外，其余的（n-1）个内角的和是2580°，则这个多边形是十七边形．

分析 根据多边形的内角和公式（n-2）•180°，可知多边形的内角和是180°的倍数，用2580°÷180°所得商的整数部分加1就是n-2的值，据此可得多边形边数．

解答 解：根据题意得：（n-2）•180°=2580°，
∴n-2=14…60，
∵除去了一个内角，
∴n-2=15，
即n=17，
故这个多边形的边数为17．
故答案为：十七．

点评 本题考查了多边形的内角和公式，利用多边形的内角和是180°的倍数是解题的关键．

练习册系列答案
相关题目
16．已知关于x的方程x2+2x=m-1无实根，试说明x2+mx=1-2m必有两个不相等的实数根的理由．
6．阅读下面的解答过程，然后作答：
有这样一类题目：将$\sqrt{a+2\sqrt{b}}$化简，若你能找到两个数 m和n，使m2+n2=a 且 mn=$\sqrt{b}$，则a+2$\sqrt{b}$ 可变为m2+n2+2mn，即变成（m+n）2，从而使得$\sqrt{a+2\sqrt{b}}$     化简．
例如：∵5+2$\sqrt{6}$=3+2+2$\sqrt{6}$=（$\sqrt{3}$）2+（$\sqrt{2}$）2+2$\sqrt{6}$=（$\sqrt{3}$+$\sqrt{2}$）2
∴$\sqrt{5+2\sqrt{6}}$=$\sqrt{（\sqrt{3}+\sqrt{2}）^{2}}$=$\sqrt{3}$+$\sqrt{2}$
请你仿照上例解下面问题（1）$\sqrt{4+2\sqrt{3}}$（2）$\sqrt{7-2\sqrt{10}}$．
3．二次根式$\sqrt{a{x}^{2}+bx+c}$（a2+b2≠0）对于x的任何值都无意义的条件是（　　）
A．a＞0，△＞0B．a＞0，△＜0C．a＜0，△＞0D．a＜0，△＜0
10．已知$\left\{\begin{array}{l}{si{n}^{2}35°+co{s}^{2}36°=\frac{5}{4}{t}^{2}}\\{co{s}^{2}35°+si{n}^{2}36°=\frac{3}{4}t}\end{array}\right.$，则实数t=-$\frac{8}{5}$或1．
20．如图，若四边形ABCD、四边形CFED都是正方形，显然图中有AG=CE，AG⊥CE．
（1）当正方形GFED绕D顺时针旋转α（0o＜α＜180o），如图2，AG=CE和AG⊥CE是否成立？若成立，请给出证明；若不成立，请说明理由．
（2）不论α为何值，CE与AG交于H，连接HD，试证明：∠GHD=45°；
（3）当α=45o，如图3的位置时，延长CE交AG于H，交AD于M．当AD=4，DG=$\sqrt{2}$时，求CH的长．
7．如图1，在平面直角坐标系中，边长为1的正方形OABC的顶点B在y轴的正半轴上，O为坐标原点．现将正方形OABC绕点O按顺时针方向旋转，旋转角为θ（0o≤θ≤45o）．
（1）当点A落到y轴正半轴上时，求边BC在旋转过程中所扫过的面积；
（2）若线段AB与y轴的交点为M（如图2），线段BC与直线y=x的交点为N．当θ=22.5°时，求此时△BMN内切圆的半径；
（3）设△MNB的周长为l，试判断在正方形OABC旋转的过程中l值是否发生变化，并说明理由．
4．如图，已知直线m的解析式为y=-$\frac{1}{2}$x+1，与x轴、y轴分别交于A，B两点，以线段AB为直角边在第一象限内作等腰Rt△ABC，且∠BAC=90°，点P为直线x=1上的动点，且△ABP的面积与△ABC的面积相等．
（1）求△ABC的面积；
（2）求点P的坐标．
5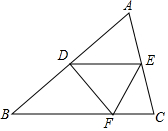．如图，点D、E分别是边AB、AC的中点，将△ADE沿着DE对折，点A落在BC边上的点F，若∠B=50°，则∠BDF的度数为（　　）
A．50°B．70°C．75°D．80°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网