题目内容
9.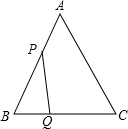 如图,在△ABC中.AB=AC=5cm,BC=6cm,点P从点沿AB向点B运动,点Q从点B沿BC向点C运动,速度都为1cm/s,P、Q两点同时出发,当点P到达点B时,运动停止,求运动几秒时,点P与点Q的连线PQ与△ABC的边垂直.
如图,在△ABC中.AB=AC=5cm,BC=6cm,点P从点沿AB向点B运动,点Q从点B沿BC向点C运动,速度都为1cm/s,P、Q两点同时出发,当点P到达点B时,运动停止,求运动几秒时,点P与点Q的连线PQ与△ABC的边垂直.
分析 分两种情况讨论①如图1,当PQ⊥BC时,有PQ∥AD,得到$\frac{PB}{AB}=\frac{BQ}{BD}$,即可得到结果;②当PQ⊥AB时,过A作AD⊥BC于D,得到△ABD∽△QBP,推出$\frac{AB}{BQ}=\frac{BD}{BP}$,即可得到结论.
解答 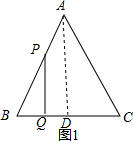 解:设运动时间为t,则AP=t,BQ=t,BP=5-t,
解:设运动时间为t,则AP=t,BQ=t,BP=5-t,
过A作AD⊥BC于D,
∵AB=AC,
∴BD=$\frac{1}{2}$BC=3cm,
①如图1,当PQ⊥BC时,
∴PQ∥AD,
∴$\frac{PB}{AB}=\frac{BQ}{BD}$,
即$\frac{5-t}{5}=\frac{t}{3}$,
解得:t=$\frac{15}{8}$,
②当PQ⊥AB时,过A作AD⊥BC于D,
∴△ABD∽△QBP,
∴$\frac{AB}{BQ}=\frac{BD}{BP}$,
即:$\frac{5}{t}=\frac{3}{5-t}$,
解得:t=$\frac{25}{8}$,
综上所述:当运动$\frac{15}{8}$s,$\frac{25}{8}$s时,点P与点Q的连线PQ与△ABC的边垂直.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,正确的周长辅助线是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
19.某种商品每件的进价为190元,按标准的九折销售时.利润率为15.2%,设这种商品的标价为每件x元,依题意列方程正确的是( )
| A. | 0.9x-190=190×0.152 | B. | 0.9x=190×0.152 | ||
| C. | 0.152x=190×0.9 | D. | 190-0.9x=190×0.152 |
17.如图,∠1>∠2的是( )
| A. |  | B. |  | C. |  | D. |  |
4.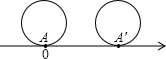 把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
 把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )| A. | π | B. | 2π | C. | 3.14 | D. | 6.28 |
1.已知直角三角形的三边a,b,c,且周长为15,斜边c=7,则△ABC的面积为( )
| A. | $\frac{15}{2}$ | B. | $\frac{15}{4}$ | C. | 15 | D. | $\frac{10}{4}$ |
 动手操作,你需要哪些工具,能在数轴上找到π,试着画出.
动手操作,你需要哪些工具,能在数轴上找到π,试着画出.