题目内容
6．
如图，在六边形ABCDEF中，AF∥CD，且∠A=120°，∠B=80°，∠E+∠F=260°，求∠C与∠D的度数．
分析 连接AC，根据平行线的性质以及多边形的内角和定理，可以求得∠D的度数；再根据多边形的内角和定理，可以求得∠BCD的度数．
解答 
解：连接AC，
∵AF∥CD，
∴∠CAF+∠ACD=180°，
∴∠D=540°-（∠CAF+∠ACD）-（∠E+∠F）=100°，
∴∠C=720°-∠A-∠B-（∠E+∠F）-∠D=160°．
点评 考查了多边形内角与外角，平行线的性质，本题需要能够熟练运用平行线的性质和三角形的内角和定理进行求解．
练习册系列答案
相关题目
（1）下面是马虎同学解的一道题
17．如图，∠1＞∠2的是（ ）
| A． |  | B． |  | C． |  | D． |  |
动手操作，你需要哪些工具，能在数轴上找到π，试着画出．
1．已知直角三角形的三边a，b，c，且周长为15，斜边c=7，则△ABC的面积为（ ）
| A． | $\frac{15}{2}$ | B． | $\frac{15}{4}$ | C． | 15 | D． | $\frac{10}{4}$ |
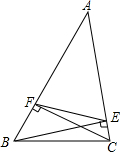如图，在△ABC中，BE、CF分别是AC、AB边上的高，∠A=45°，求S△AEF：S四边形FBCE．
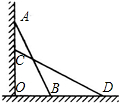如图，一架云梯AB长25m，斜靠在一竖直的墙AO上，这时梯子底端B离墙的距离BO是7m，如果梯子的顶端A沿墙下滑了4m，那么梯子底部在水平方向也滑动了4m吗？请给以说明．