题目内容
13. 如图,已知E为?ABCD的边CD上一点,BE交AD的延长线于点F.若S?ABCD:S△AEF=5:1,求$\frac{AF}{DF}$的值.
如图,已知E为?ABCD的边CD上一点,BE交AD的延长线于点F.若S?ABCD:S△AEF=5:1,求$\frac{AF}{DF}$的值.
分析 根据S△ABE=$\frac{1}{2}$S平行四边形ABCD,S?ABCD:S△AEF=5:1,于是得到S△ABE:S△AEF=2.5:1=5:2,根据等高三角形面积的比等于底的比得到BE:EF=5:2,然后根据相似三角形的判定和性质即可得到结论.
解答 解:∵E为?ABCD的边CD上一点,
∴S△ABE=$\frac{1}{2}$S平行四边形ABCD,
∵S?ABCD:S△AEF=5:1,
∴S△ABE:S△AEF=2.5:1=5:2,
∴BE:EF=5:2,
在?ABCD中,∵AD=BC,AD∥BC,
∴△DEF∽△CEB,
∴$\frac{DF}{BC}=\frac{EF}{BE}$=$\frac{2}{5}$,
∴$\frac{DF}{AD}=\frac{2}{5}$,
∴$\frac{DF}{AF}=\frac{2}{7}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,熟记各定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.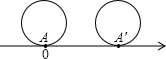 把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
 把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )| A. | π | B. | 2π | C. | 3.14 | D. | 6.28 |
1.已知直角三角形的三边a,b,c,且周长为15,斜边c=7,则△ABC的面积为( )
| A. | $\frac{15}{2}$ | B. | $\frac{15}{4}$ | C. | 15 | D. | $\frac{10}{4}$ |
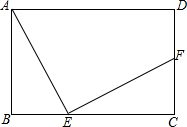 如图,已知长方形ABCD的周长为20,AB=4,点E在BC上,AE⊥EF,AE=EF,求CF的长.
如图,已知长方形ABCD的周长为20,AB=4,点E在BC上,AE⊥EF,AE=EF,求CF的长.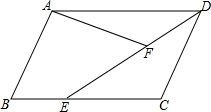 如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.
如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.
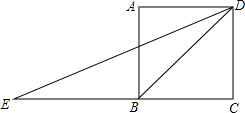 如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少?
如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少?