题目内容
 如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹的角记为∠1,边AC与直线l所夹的角记为∠2.(友情提示:等边三角形每个内角都等于60°)
如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹的角记为∠1,边AC与直线l所夹的角记为∠2.(友情提示:等边三角形每个内角都等于60°)(1)当∠1=24°,求∠2的大小;
(2)写出∠1、∠2满足的等式关系,并说明你写出的等式关系正确.
考点:平行线的性质
专题:
分析:(1)根据平行线的性质可得∠1=∠3=24°,再根据等边三角形的性质可得∠3的度数,再次利用平行线的性质可得∠2的度数;
(2)根据平行线的性质可得∠1=∠3,∠4=∠2,因此∠2+∠1=∠3+∠4=60°.
(2)根据平行线的性质可得∠1=∠3,∠4=∠2,因此∠2+∠1=∠3+∠4=60°.
解答:(1) 解:如图,∵m∥n,
解:如图,∵m∥n,
∴∠1=∠3=24°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠4=60°-24°=36°,
∵l∥m,
∴∠4=∠2=35°.
(2)∠1+∠2=60°.
证明:∵m∥n,
∴∠1=∠3,
∵l∥m,
∴∠4=∠2.
∵∠ACB=∠3+∠4=60°,
∴∠1+∠2=60°.
 解:如图,∵m∥n,
解:如图,∵m∥n,∴∠1=∠3=24°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠4=60°-24°=36°,
∵l∥m,
∴∠4=∠2=35°.
(2)∠1+∠2=60°.
证明:∵m∥n,
∴∠1=∠3,
∵l∥m,
∴∠4=∠2.
∵∠ACB=∠3+∠4=60°,
∴∠1+∠2=60°.
点评:此题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等,同位角相等.

练习册系列答案
相关题目
使两个直角三角形全等的条件是( )
| A、一组锐角相等 |
| B、斜边对应相等 |
| C、一条直角边对应相等 |
| D、两条直角边对应相等 |
 如图是一个正方体的表面展开图,则与“中”字所在的图相对的面上标的字是( )
如图是一个正方体的表面展开图,则与“中”字所在的图相对的面上标的字是( )| A、我 | B、的 | C、梦 | D、国 |
 如图,已知线段AB=12cm,线段BC=4cm,D是线段AB的中点,E是线段BC的中点,则线段DE长为
如图,已知线段AB=12cm,线段BC=4cm,D是线段AB的中点,E是线段BC的中点,则线段DE长为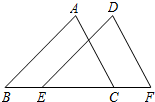 己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.
己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.
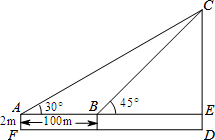 如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)
如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)