题目内容
如图,四边形ABCD中,AD∥BC,∠A=2∠C,求证:AB+AD=BC.(有不同证法)


考点:平行四边形的判定与性质
专题:
分析:可过A作AE∥CD交BC于点E,证明四边形ADCE为平行四边形,再证明BA=BE即可;也可过D作DF∥BA交BC于点F,证明四边形ABFD为平行四边形,再证明DF=CF即可.
解答:解:方法一:
如图1,过A作AE∥CD交BC于点E,

∵AD∥BC,
∴四边形ADCE为平行四边形,
∴AD=EC,
∴∠C=∠AEB,且∠DAE=∠AEB,
∴∠C=∠DAE,
又∵∠DAB=2∠C,
∴∠BAE=∠C=∠BEA,
∴AB=BE,
∴BC=CE+BE=AD+AB.
方法二:
如图2,过D作DF∥AB,

∵AD∥BC,
∴四边形ABFD为平行四边形,
∴AD=BF,AB=DF,
∴∠A+∠B=180°,∠B=∠DFC,
∴∠A+∠DFC=180°,
又∵∠A=2∠C,
∴2∠C+∠DFC=180°,
又∵∠DFC+∠C+∠FDC=180°,
∴∠C=∠FDC,
∴DF=FC,
∴BC=BF+FC=AD+AB.
如图1,过A作AE∥CD交BC于点E,

∵AD∥BC,
∴四边形ADCE为平行四边形,
∴AD=EC,
∴∠C=∠AEB,且∠DAE=∠AEB,
∴∠C=∠DAE,
又∵∠DAB=2∠C,
∴∠BAE=∠C=∠BEA,
∴AB=BE,
∴BC=CE+BE=AD+AB.
方法二:
如图2,过D作DF∥AB,

∵AD∥BC,
∴四边形ABFD为平行四边形,
∴AD=BF,AB=DF,
∴∠A+∠B=180°,∠B=∠DFC,
∴∠A+∠DFC=180°,
又∵∠A=2∠C,
∴2∠C+∠DFC=180°,
又∵∠DFC+∠C+∠FDC=180°,
∴∠C=∠FDC,
∴DF=FC,
∴BC=BF+FC=AD+AB.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行?四边形为平行四边形,②两组对边分别相等?四边形为平行四边形,③一组对边平行且相等?四边形为平行四边形,④两组对角分别相等?四边形为平行四边形,⑤对角线互相平分?四边形为平行四边形.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 如图,在数轴上有a,b两个实数,则下列结论中,正确的是( )
如图,在数轴上有a,b两个实数,则下列结论中,正确的是( )| A、a>-b |
| B、|a|<|b| |
| C、-ab>0 |
| D、a+b>0 |
 如图是一个物体的俯视图,则它所对应的物体是( )
如图是一个物体的俯视图,则它所对应的物体是( )A、 |
B、 |
C、 |
D、 |
 如图,△ABC外接圆的圆心坐标为
如图,△ABC外接圆的圆心坐标为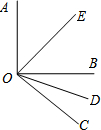 已知,如图,∠AOB=90°,∠EOD=70°,OE、OD分别是∠AOB和∠BOC的角平分线,求∠BOC的度数.
已知,如图,∠AOB=90°,∠EOD=70°,OE、OD分别是∠AOB和∠BOC的角平分线,求∠BOC的度数.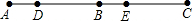 问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长.请补全以下解答过程.
问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长.请补全以下解答过程. 如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹的角记为∠1,边AC与直线l所夹的角记为∠2.(友情提示:等边三角形每个内角都等于60°)
如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹的角记为∠1,边AC与直线l所夹的角记为∠2.(友情提示:等边三角形每个内角都等于60°) 如图,已知AB∥CD,CE∥BF.求证:∠B=∠C.
如图,已知AB∥CD,CE∥BF.求证:∠B=∠C. 如图,Rt△ABC≌△CDE,∠B=∠D=90°,且B、C、D三点在同一条直线上,试利用这个图形证明勾股定理公式.
如图,Rt△ABC≌△CDE,∠B=∠D=90°,且B、C、D三点在同一条直线上,试利用这个图形证明勾股定理公式.