题目内容
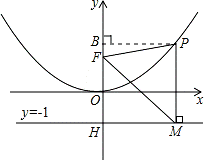
二次函数图象的顶点在原点O,经过点A(1,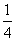 );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
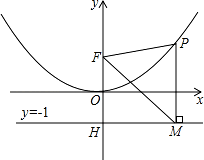
解答:(1)解:∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1,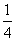 )代入y=ax2得:a=
)代入y=ax2得:a=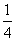 ,
,
∴二次函数的解析式 为y=
为y=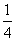 x2;
x2;
(2)证明:∵点P在抛物线y=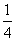 x2上,
x2上,
∴可设点P的坐标为(x,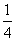 x2),
x2),
过点P作P B⊥y轴于点B,则BF=
B⊥y轴于点B,则BF=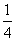 x2﹣1,PB=x,
x2﹣1,PB=x,
∴Rt△BPF中,
PF=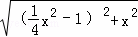 =
=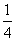 x2+1,
x2+1,
∵PM⊥直线y=﹣1,
∴PM=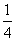 x2+1,
x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥x轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)解:当△FPM是等边三角形时,∠PMF=60°,
 ∴∠FMH=30°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴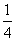 x2+1=4,
x2+1=4,
解得:x=±2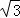 ,
,
∴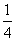 x
x 2=
2=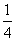 ×12=3,
×12=3,
∴满足条件的点P的坐标为(2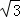 ,3)或(﹣2
,3)或(﹣2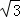 ,3).
,3).

练习册系列答案
相关题目
 x2+x+c与x轴没有交点.
x2+x+c与x轴没有交点. 称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;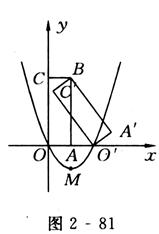
 D、y=x2
D、y=x2 图象和x轴有交点,则k的取值范围是
图象和x轴有交点,则k的取值范围是 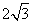 ,求OP的长.
,求OP的长.