题目内容
如图，AD、BE分别是△ABC的高和角平分线，AD、BE相交于点F，∠BAC=70°，∠C=60°，则∠BFD的度数是（ ）| A、25° | B、35° |
| C、65° | D、75° |
考点：三角形内角和定理
专题：
分析：根据高线的定义可得∠ADB=90°，然后根据∠BAC=70°，∠C=60°，求出∠ABC的度数，再根据角平分线的定义求出∠FBD，然后利用三角形的内角和等于180°列式计算即可得解．
解答：解：∵AD是高线，
∴∠ADB=90°
∵∠BAC=70°，∠C=60°，
∴∠ABC=180°-60°-70°=50°，
∵BE是角平分线，
∴∠ABC=2∠FBD=40°，
∴∠FBD=25°，
在△FBD中，∠FBD=180°-90°-25°=65°，
故选：C．
∴∠ADB=90°
∵∠BAC=70°，∠C=60°，
∴∠ABC=180°-60°-70°=50°，
∵BE是角平分线，
∴∠ABC=2∠FBD=40°，
∴∠FBD=25°，
在△FBD中，∠FBD=180°-90°-25°=65°，
故选：C．
点评：本题考查了三角形的内角和定理，角平分线的定义，高线的定义，熟记概念与定理并准确识图是解题的关键．
练习册系列答案
相关题目
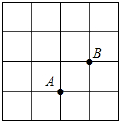已知在正方形网格中，每个小方格都是边长为1的正方形，A、B两点在格点上，位置如图，点C也在格点上，且△ABC为等腰三角形，则点C的个数为（ ）
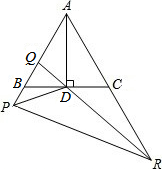如图，在等边△ABC中，AD⊥BC于D，点P在AB的延长线上，点Q在AB上，∠PDQ=60°，QD的延长线交AC的延长线于R（PB＜CR）．若AB=4，PR=7，则PQ=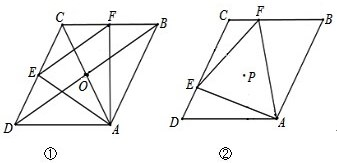
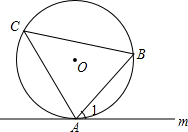如图，直线m与⊙O相切于点A，∠C是弦AB所对的圆周角，试判断∠C与∠1的大小关系．
已知线段a，b，c．