题目内容
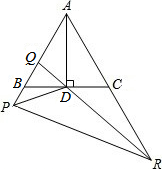 如图,在等边△ABC中,AD⊥BC于D,点P在AB的延长线上,点Q在AB上,∠PDQ=60°,QD的延长线交AC的延长线于R(PB<CR).若AB=4,PR=7,则PQ=
如图,在等边△ABC中,AD⊥BC于D,点P在AB的延长线上,点Q在AB上,∠PDQ=60°,QD的延长线交AC的延长线于R(PB<CR).若AB=4,PR=7,则PQ=考点:相似形综合题,正弦定理与余弦定理,全等三角形的判定与性质,等边三角形的判定与性质,相似三角形的判定与性质
专题:
分析:如图1,易证BD=CD=2,∠PBD=∠DCR=∠PDR=120°,从而证到△PBD∽△PDR∽△DCR,进而可得到∠3=∠4,∠5=∠6,PD2=PB•PR,PB•CR=BD•DC=4①.在PR上取两点E、F,使得PE=PB、RF=RC,如图2,从而可证到△BPD≌△EPD,则有BD=ED=2,∠PBD=∠PED=120°,∠DEF=60°.同理可得DF=DC=2,即可证到△DEF是等边三角形,则有EF=DE=2,从而有PE+RF=5即PB+RC=5②.解①和②就可求出PB的长,进而就可求出PD的长.易证△QBD∽△QDP,根据相似三角形的性质可得
=(
)2=
.由
=
(等高)可得
=
,再根据PB=QP-QB=1即可求出QP的长.
| S△QBD |
| S△QDP |
| BD |
| DP |
| 4 |
| 7 |
| S△QBD |
| S△QDP |
| QB |
| QP |
| QB |
| QP |
| 4 |
| 7 |
解答:解:如图1,
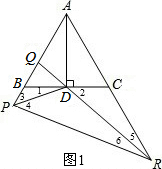
∵△ABC是等边三角形,AD⊥BC,
∴∠ABC=∠ACB=60°,BD=CD=
BC=2,
∴∠PBD=∠DCR=120°.
∵∠QDP=60°,∴∠PDR=120°,
∴∠PBD=∠DCR=∠PDR=120°,
∴∠1+∠2=60°=∠1+∠3,
∴∠2=∠3,
∴△PBD∽△DCR,
∴
=
,
∴
=
.
∵∠PBD=∠PDR,
∴△PBD∽△PDR,
∴△PBD∽△PDR∽△DCR,
∴∠3=∠4,∠5=∠6,
=
,
=
,
∴PD2=PB•PR,PB•CR=BD•DC=4.
在PR上取两点E、F,使得PE=PB、RF=RC,如图2,
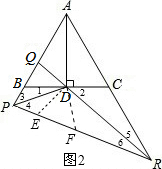
在△BPD和△EPD中,
,
∴△BPD≌△EPD(SAS),
∴BD=ED=2,∠PBD=∠PED=120°,
∴∠DEF=60°.
同理可得;DF=DC=2,
∴ED=FD,
∴△DEF是等边三角形,
∴EF=DE=2.
∵PR=7,∴PE+RF=5,
∴PB+RC=5.
∵PB•CR=4,PB<CR,
∴PB=1,RC=4,
∴PD2=PB•PR=1×7=7,
∴PD=
.
∵∠BQD=∠DQP,∠QBD=∠QDP=60°,
∴△QBD∽△QDP,
∴
=(
)2=
.
又∵
=
(等高),
∴
=
,
∴QB=
QP,
∴PB=QP-QB=QP-
QP=
QP=1,
∴QP=
.
故答案为:
.

∵△ABC是等边三角形,AD⊥BC,
∴∠ABC=∠ACB=60°,BD=CD=
| 1 |
| 2 |
∴∠PBD=∠DCR=120°.
∵∠QDP=60°,∴∠PDR=120°,
∴∠PBD=∠DCR=∠PDR=120°,
∴∠1+∠2=60°=∠1+∠3,
∴∠2=∠3,
∴△PBD∽△DCR,
∴
| PB |
| DC |
| PD |
| DR |
∴
| PB |
| BD |
| PD |
| DR |
∵∠PBD=∠PDR,
∴△PBD∽△PDR,
∴△PBD∽△PDR∽△DCR,
∴∠3=∠4,∠5=∠6,
| BP |
| PD |
| PD |
| PR |
| PB |
| DC |
| BD |
| CR |
∴PD2=PB•PR,PB•CR=BD•DC=4.
在PR上取两点E、F,使得PE=PB、RF=RC,如图2,

在△BPD和△EPD中,
|
∴△BPD≌△EPD(SAS),
∴BD=ED=2,∠PBD=∠PED=120°,
∴∠DEF=60°.
同理可得;DF=DC=2,
∴ED=FD,
∴△DEF是等边三角形,
∴EF=DE=2.
∵PR=7,∴PE+RF=5,
∴PB+RC=5.
∵PB•CR=4,PB<CR,
∴PB=1,RC=4,
∴PD2=PB•PR=1×7=7,
∴PD=
| 7 |
∵∠BQD=∠DQP,∠QBD=∠QDP=60°,
∴△QBD∽△QDP,
∴
| S△QBD |
| S△QDP |
| BD |
| DP |
| 4 |
| 7 |
又∵
| S△QBD |
| S△QDP |
| QB |
| QP |
∴
| QB |
| QP |
| 4 |
| 7 |
∴QB=
| 4 |
| 7 |
∴PB=QP-QB=QP-
| 4 |
| 7 |
| 3 |
| 7 |
∴QP=
| 7 |
| 3 |
故答案为:
| 7 |
| 3 |
点评:本题主要考查了等边三角形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质等知识,综合性强,难度大.解决本题的关键是通过构造全等三角形得到PB+CR=5,由△PBD∽△DCR得到PB•CR=4,进而求出PB的长.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )| A、59° | B、60° |
| C、56° | D、22° |
 如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )
如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )| A、25° | B、35° |
| C、65° | D、75° |
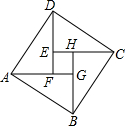 如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )
如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )| A、1:5 | B、1:25 |
| C、5:1 | D、25:1 |
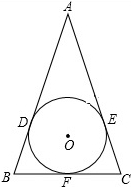 如图,圆O是△ABC的内切圆,切点分别为D,E,F,AB=AC=13,BC=10,求圆O的半径.
如图,圆O是△ABC的内切圆,切点分别为D,E,F,AB=AC=13,BC=10,求圆O的半径.