题目内容
如图,已知菱形ABCD的边长为2,∠ADC=60°,等边三角形△AEF两边分别交边DC,CB于点E,F.
(1)求证:△ADE≌△ACF;
(2)如图2所示,若点E,F始终分别在边DC,CB上移动,记等边△AEF面积为S,则S是否存在最小值?若存在,值为多少;若不存在,请说明理由;
(3)若S存在最小值,对角线AC上是否存在点P,使△PDE的周长最小?若存在,请求出这个最小值;若不存在,请说明理由.
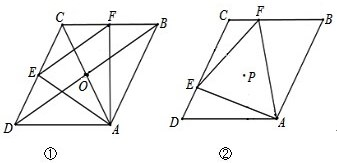
(1)求证:△ADE≌△ACF;
(2)如图2所示,若点E,F始终分别在边DC,CB上移动,记等边△AEF面积为S,则S是否存在最小值?若存在,值为多少;若不存在,请说明理由;
(3)若S存在最小值,对角线AC上是否存在点P,使△PDE的周长最小?若存在,请求出这个最小值;若不存在,请说明理由.

考点:四边形综合题
专题:综合题
分析:(1)根据菱形的性质判断△ADC为等边三角形,则AD=AC,再根据边三角形的性质得∠EAF=60°,AE=AF,易得∠DAE=∠CAF,然后根据“SAS”可证明△ADE≌△ACF;
(2)设DE=x,利用含30度的直角三角形三边的关系得到DH=
x,EH=
x,则AH=AD-DH=2-
x,再在Rt△AEH中根据勾股定理计算出AE2=x2-2x+4,然后根据等边三角形的面积公式得到S=
(x2-2x+4),再利用配方得到S=
(x-1)2+
,然后根据非负数的性质即可得到当x=1时,S有最小值
;
(3)如图③,作EQ⊥BC于Q,连接BE交AC于P,连接PD,由菱形的性质得AC垂直平分BD,则PD=PB,所以PE+PD=PE+PB=BE,根据两点之间线段最短得到此时△PDE的周长最小,在Rt△CQE中,利用含30度的直角三角形三边的关系得到CQ=
,QE=
,然后在Rt△BEQ中,根据勾股定理可计算出BE=
,于是得到此时△PDE的周长为1+
,即△PDE的周长最小值为1+
.
(2)设DE=x,利用含30度的直角三角形三边的关系得到DH=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
3
| ||
| 4 |
3
| ||
| 4 |
(3)如图③,作EQ⊥BC于Q,连接BE交AC于P,连接PD,由菱形的性质得AC垂直平分BD,则PD=PB,所以PE+PD=PE+PB=BE,根据两点之间线段最短得到此时△PDE的周长最小,在Rt△CQE中,利用含30度的直角三角形三边的关系得到CQ=
| 1 |
| 2 |
| ||
| 2 |
| 7 |
| 7 |
| 7 |
解答:(1)证明:∵四边形ABCD为菱形,
∴DC=DA,
∵∠ADC=60°,
∴△ADC为等边三角形,
∴AD=AC,
∵△AEF为等边三角形,
∴∠EAF=60°,AE=AF,
∵∠DAE+∠EAC=60°,∠CAF+∠EAC=60°,
∴∠DAE=∠CAF,
在△ADE和△ACF中,
,
∴△ADE≌△ACF(ASA);
(2)解: 存在.
存在.
设DE=x,
在Rt△DEH中,∵∠D=60°,
∴∠DHE=30°,
∴DH=
x,EH=
x,
∴AH=AD-DH=2-
x,
在Rt△AEH中,AE2=AH2+EH2=(2-
x)2+(
x)2=x2-2x+4,
∴S=
AE2=
(x2-2x+4)=
(x-1)2+
,
∴当x=1时,S有最小值,最小值为
;
(3)如图, 作EQ⊥BC于Q,连接BE交AC于P,连接PD,
作EQ⊥BC于Q,连接BE交AC于P,连接PD,
∵四边形ABCD为菱形,
∴AC垂直平分BD,
∴PD=PB,
∴PE+PD=PE+PB=BE,
∴此时△PDE的周长最小,
∵DE=1,
∴EC=1,
∵∠BCE=120°,
∴∠QCE=60°,
在Rt△CQE中,CQ=
CE=
,QE=
CQ=
,
∴BQ=BC+CQ=2+
=
,
在Rt△BEQ中,BE=
=
,
∴此时△PDE的周长=DE+PE+PD=DE+BE=1+
.
∴DC=DA,
∵∠ADC=60°,
∴△ADC为等边三角形,
∴AD=AC,
∵△AEF为等边三角形,
∴∠EAF=60°,AE=AF,
∵∠DAE+∠EAC=60°,∠CAF+∠EAC=60°,
∴∠DAE=∠CAF,
在△ADE和△ACF中,
|
∴△ADE≌△ACF(ASA);
(2)解:
 存在.
存在.设DE=x,
在Rt△DEH中,∵∠D=60°,
∴∠DHE=30°,
∴DH=
| 1 |
| 2 |
| ||
| 2 |
∴AH=AD-DH=2-
| 1 |
| 2 |
在Rt△AEH中,AE2=AH2+EH2=(2-
| 1 |
| 2 |
| ||
| 2 |
∴S=
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
3
| ||
| 4 |
∴当x=1时,S有最小值,最小值为
3
| ||
| 4 |
(3)如图,
 作EQ⊥BC于Q,连接BE交AC于P,连接PD,
作EQ⊥BC于Q,连接BE交AC于P,连接PD,∵四边形ABCD为菱形,
∴AC垂直平分BD,
∴PD=PB,
∴PE+PD=PE+PB=BE,
∴此时△PDE的周长最小,
∵DE=1,
∴EC=1,
∵∠BCE=120°,
∴∠QCE=60°,
在Rt△CQE中,CQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴BQ=BC+CQ=2+
| 1 |
| 2 |
| 5 |
| 2 |
在Rt△BEQ中,BE=
| QE2+BQ2 |
| 7 |
∴此时△PDE的周长=DE+PE+PD=DE+BE=1+
| 7 |
点评:本题考查了四边形的综合题:熟练掌握菱形的性质、等边三角形的判定与性质和非负数的性质;会运用配方法解决代数式的最值问题;利用对称解决最小距离之和的问题;会应用含30度的直角三角形三边的关系和勾股定理进行几何计算.

练习册系列答案
相关题目
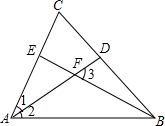 如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )| A、59° | B、60° |
| C、56° | D、22° |
 如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )
如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )| A、25° | B、35° |
| C、65° | D、75° |
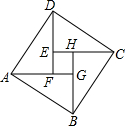 如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )
如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )| A、1:5 | B、1:25 |
| C、5:1 | D、25:1 |

 如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.
如图,在△ABC中,∠A=62°,∠1=20°,∠2=35°.求∠BDC的度数.