题目内容
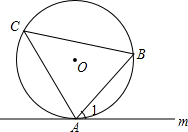 如图,直线m与⊙O相切于点A,∠C是弦AB所对的圆周角,试判断∠C与∠1的大小关系.
如图,直线m与⊙O相切于点A,∠C是弦AB所对的圆周角,试判断∠C与∠1的大小关系.考点:切线的性质,圆周角定理,弦切角定理
专题:
分析:连接AO并延长交圆于E,连接BE,根据直径所对的圆周角是直角,可以得到∠E+∠EAB=90°;再根据AB是切线可以得到∠EAB+∠1=90°,所以∠E=∠1,最后根据等弧所对的圆周角相等就可以的得到所要的结论.
解答: 解:如图,作直径AE,连接EB,
解:如图,作直径AE,连接EB,
∠ACB=∠E;
证明:∵AE是⊙O的直径,
∴∠EAB+∠E=∠EBA=90°;
又∵AB是⊙O的切线,
∴∠EAB+∠1=90°,
∴∠1=∠E;
∴∠C=∠1.
 解:如图,作直径AE,连接EB,
解:如图,作直径AE,连接EB,∠ACB=∠E;
证明:∵AE是⊙O的直径,
∴∠EAB+∠E=∠EBA=90°;
又∵AB是⊙O的切线,
∴∠EAB+∠1=90°,
∴∠1=∠E;
∴∠C=∠1.
点评:本题综合运用了切线的性质、等角的余角相等以及圆周角定理的推论,熟记定理是解题的关键.

练习册系列答案
相关题目
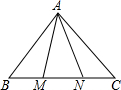 如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANC=120°,则∠MAC的度数等于( )
如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANC=120°,则∠MAC的度数等于( )| A、120° | B、70° |
| C、60° | D、50°. |
 如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )
如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )| A、25° | B、35° |
| C、65° | D、75° |
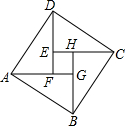 如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )
如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )| A、1:5 | B、1:25 |
| C、5:1 | D、25:1 |
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
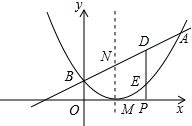 已知二次函数的图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.
已知二次函数的图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.