题目内容
①半径为13cm圆内的两条平行弦分别为10cm和24cm长,则两条平行弦之间距离是 ;
②△ABC是⊙O的内接三角形,AB=AC,BC=20cm,点O到BC的距离为6cm,则△ABC的面积是 ;
③两个圆相切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径为 ;
④若O为△ABC的外心,∠C=n°,用n°表示∠AOB为 ;
⑤OA、OB是⊙O的半径,且互相垂直,延长OB到C,使BC=OB,CD是⊙O的切线,D为切点,则∠OAD的度数为 ;
⑥已知两圆的半径分别为4和5,公共弦长6,则两圆的圆距为 ;
⑦若一个点到圆的最长距离为a,最短距离为b,则此圆的半径 .
②△ABC是⊙O的内接三角形,AB=AC,BC=20cm,点O到BC的距离为6cm,则△ABC的面积是
③两个圆相切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径为
④若O为△ABC的外心,∠C=n°,用n°表示∠AOB为
⑤OA、OB是⊙O的半径,且互相垂直,延长OB到C,使BC=OB,CD是⊙O的切线,D为切点,则∠OAD的度数为
⑥已知两圆的半径分别为4和5,公共弦长6,则两圆的圆距为
⑦若一个点到圆的最长距离为a,最短距离为b,则此圆的半径
考点:圆的综合题
专题:分类讨论
分析:①可分AB和CD在O的两旁和同旁两种情况讨论,然后运用垂径定理和勾股定理就可解决问题;
②可分圆心O在△ABC的外部和内部两种情况讨论,然后运用垂径定理和勾股定理就可解决问题;
③由于两圆的圆心距小于一个圆的半径,因此两圆内切,可分所求圆的半径大于5和小于5两种情况讨论,然后运用切线的性质就可解决问题;
④可分点C与点O在AB的同侧和异侧两种情况讨论,然后运用圆周角定理和圆内接四边形的性质就可解决问题;
⑤可分点A与点D在直线OC的同侧和异侧两种情况讨论,然后运用切线的性质和特殊三角函数值就可解决问题;
⑥可分两圆的圆心在公共弦的两侧和同侧两种情况讨论,然后运用相交两圆的性质和勾股定理即可解决问题;
⑦只需可分点在圆内和圆外两种情况讨论即可解决问题.
②可分圆心O在△ABC的外部和内部两种情况讨论,然后运用垂径定理和勾股定理就可解决问题;
③由于两圆的圆心距小于一个圆的半径,因此两圆内切,可分所求圆的半径大于5和小于5两种情况讨论,然后运用切线的性质就可解决问题;
④可分点C与点O在AB的同侧和异侧两种情况讨论,然后运用圆周角定理和圆内接四边形的性质就可解决问题;
⑤可分点A与点D在直线OC的同侧和异侧两种情况讨论,然后运用切线的性质和特殊三角函数值就可解决问题;
⑥可分两圆的圆心在公共弦的两侧和同侧两种情况讨论,然后运用相交两圆的性质和勾股定理即可解决问题;
⑦只需可分点在圆内和圆外两种情况讨论即可解决问题.
解答:解:①若AB和CD在O的两旁,如图①a,
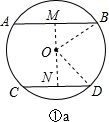
过O作MN⊥AB于M,交CD于N,连接OB、OD,
∵AB∥CD,
∴MN⊥CD,
∴BM=
AB=12cm,DN=
CD=5cm,
∵OB=OD=13cm,
∴OM=
=5cm,
同理ON=12cm,
∴MN=OM+ON=5+12=17(cm),
若AB和CD在O的同旁,如图①b,
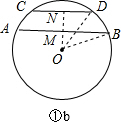
同理可得:MN=12-5=7(cm).
故答案为:17cm或7cm.
②若圆心O在△ABC的外部,连接OA、OB,如图②a,
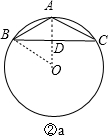
则有OA⊥BC,BD=DC=
BC=10,
∴OB2=BD2+OD2=100+36=136,
∴OB=2
,
∴AD=OA-OD=OB-OD=2
-6,
∴S△ABC=
BC•AD=
×20×(2
-6)=20
-60(cm2).
若圆心O在△ABC的内部,连接OA并延长交BC于D,连接OB,如图②b,
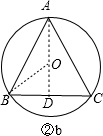
则有AD⊥BC,BD=DC=
BC=10,
同理可得:S△ABC=
BC•AD=
×20×(2
+6)=20
+60(cm2).
故答案为:(20
-60)cm2或(20
+60)cm2.
③不妨设⊙O2的半径为5,由题可得O1O2=2.
∵O1O2<5,∴两个圆相内切.
若⊙O2的半径比⊙O1的半径大,连接AO2,如图③a,
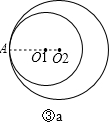
则AO2必过点O1.
∴AO1=AO2-O1O2=5-2=3.
若⊙O2的半径比⊙O1的半径小,连接AO1,如图③b,
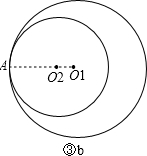
则AO1必过点O2,
同理可得:AO1=AO2+O1O2=5+2=7.
故答案为:3或7.
④若点C与点O在AB的同侧,如图④a,
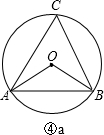
则∠AOB=2∠C=2n°.
若点C与点O在AB的异侧,如图④b,
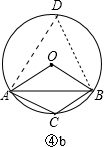
在弦AB所对的优弧上取一点D,连接DA、DB,
则有∠C+∠D=180°,∠AOB=2∠D.
∴∠AOB=2(180°-∠C)=2(180°-n°)=360°-2n°.
故答案为:2n°或360°-2n°.
⑤若点A与点D在直线OC的同侧,连接OD,如图⑤a,
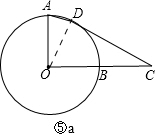
∵CD与⊙O相切于D,∴OD⊥DC即∠ODC=90°.
∵BC=OB,OD=OB,
∴OC=2OD,
∴cos∠DOC=
=
,
∴∠DOC=60°.
∵OA⊥OB即∠AOB=90°,
∴∠AOD=30°.
∵OA=OD,∴∠OAD=∠ODA=
=75°.
若点A与点D在直线OC的异侧,连接OD,如图⑤b,
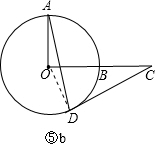
同理可得∠OAD=15°.
故答案为:75°或15°.
⑥不妨设⊙O1的半径为5,⊙O2的半径为4.
若圆心O1与圆心O2在公共弦AB的两侧,连接AO1、AO2,如图⑥a,
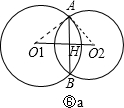
则有O1O2⊥AB,AH=BH=
AB=3.
在Rt△AHO1中,
O1H=
=
=4.
同理可得O2H=
,
∴O1O2=O1H+O2H=4+
.
若圆心O1与圆心O2在公共弦AB的同侧,连接AO1、AO2,如图⑥b,
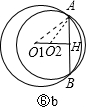
同理可得:O1O2=O1H-O2H=4-
.
故答案为:4+
或4-
.
⑦若点P在圆外,连接PO交⊙O于点A,延长PO与⊙O交于点B,如图⑦a,
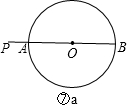
则PB=a,PA=b,
∴AB=PB-PA=a-b,
∴OA=
AB=
.
若点P在圆内,延长OP交⊙O于点A,延长PO与⊙O交于点B,如图⑦b,
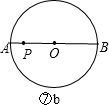
同理可得:OA=
AB=
.
故答案为:
或
.

过O作MN⊥AB于M,交CD于N,连接OB、OD,
∵AB∥CD,
∴MN⊥CD,
∴BM=
| 1 |
| 2 |
| 1 |
| 2 |
∵OB=OD=13cm,
∴OM=
| OB2-BM2 |
同理ON=12cm,
∴MN=OM+ON=5+12=17(cm),
若AB和CD在O的同旁,如图①b,

同理可得:MN=12-5=7(cm).
故答案为:17cm或7cm.
②若圆心O在△ABC的外部,连接OA、OB,如图②a,

则有OA⊥BC,BD=DC=
| 1 |
| 2 |
∴OB2=BD2+OD2=100+36=136,
∴OB=2
| 34 |
∴AD=OA-OD=OB-OD=2
| 34 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 34 |
| 34 |
若圆心O在△ABC的内部,连接OA并延长交BC于D,连接OB,如图②b,

则有AD⊥BC,BD=DC=
| 1 |
| 2 |
同理可得:S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 34 |
| 34 |
故答案为:(20
| 34 |
| 34 |
③不妨设⊙O2的半径为5,由题可得O1O2=2.
∵O1O2<5,∴两个圆相内切.
若⊙O2的半径比⊙O1的半径大,连接AO2,如图③a,

则AO2必过点O1.
∴AO1=AO2-O1O2=5-2=3.
若⊙O2的半径比⊙O1的半径小,连接AO1,如图③b,

则AO1必过点O2,
同理可得:AO1=AO2+O1O2=5+2=7.
故答案为:3或7.
④若点C与点O在AB的同侧,如图④a,

则∠AOB=2∠C=2n°.
若点C与点O在AB的异侧,如图④b,

在弦AB所对的优弧上取一点D,连接DA、DB,
则有∠C+∠D=180°,∠AOB=2∠D.
∴∠AOB=2(180°-∠C)=2(180°-n°)=360°-2n°.
故答案为:2n°或360°-2n°.
⑤若点A与点D在直线OC的同侧,连接OD,如图⑤a,

∵CD与⊙O相切于D,∴OD⊥DC即∠ODC=90°.
∵BC=OB,OD=OB,
∴OC=2OD,
∴cos∠DOC=
| OD |
| OC |
| 1 |
| 2 |
∴∠DOC=60°.
∵OA⊥OB即∠AOB=90°,
∴∠AOD=30°.
∵OA=OD,∴∠OAD=∠ODA=
| 180°-30° |
| 2 |
若点A与点D在直线OC的异侧,连接OD,如图⑤b,

同理可得∠OAD=15°.
故答案为:75°或15°.
⑥不妨设⊙O1的半径为5,⊙O2的半径为4.
若圆心O1与圆心O2在公共弦AB的两侧,连接AO1、AO2,如图⑥a,

则有O1O2⊥AB,AH=BH=
| 1 |
| 2 |
在Rt△AHO1中,
O1H=
| O1A2-AH2 |
| 52-32 |
同理可得O2H=
| 7 |
∴O1O2=O1H+O2H=4+
| 7 |
若圆心O1与圆心O2在公共弦AB的同侧,连接AO1、AO2,如图⑥b,

同理可得:O1O2=O1H-O2H=4-
| 7 |
故答案为:4+
| 7 |
| 7 |
⑦若点P在圆外,连接PO交⊙O于点A,延长PO与⊙O交于点B,如图⑦a,

则PB=a,PA=b,
∴AB=PB-PA=a-b,
∴OA=
| 1 |
| 2 |
| a-b |
| 2 |
若点P在圆内,延长OP交⊙O于点A,延长PO与⊙O交于点B,如图⑦b,

同理可得:OA=
| 1 |
| 2 |
| a+b |
| 2 |
故答案为:
| a-b |
| 2 |
| a+b |
| 2 |
点评:本题组属于圆中的多解问题,考查了垂径定理、圆周角定理、圆的内接四边形的性质、切线的性质、相交两圆的性质、相切两圆的性质、勾股定理等知识,而正确进行分类是解决此类题的关键.

练习册系列答案
相关题目
 如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )
如图,AD、BE分别是△ABC的高和角平分线,AD、BE相交于点F,∠BAC=70°,∠C=60°,则∠BFD的度数是( )| A、25° | B、35° |
| C、65° | D、75° |
 如图AE=AD,要证明△ABD≌△AEC,
如图AE=AD,要证明△ABD≌△AEC,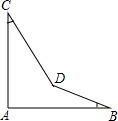 如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.
如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.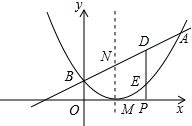 已知二次函数的图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.
已知二次函数的图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.