题目内容
2.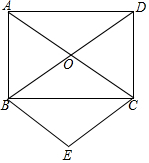 如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E.(1)求AB,AC的长;
(2)判断四边形BOCE的形状.
分析 (1)由矩形的性质可△ABC为直角三角形,由条件结合勾股定理可求得AB、AC的长;
(2)由条件可先判定四边形BOCE为平行四边形,再结合矩形的性质可判定其为菱形.
解答 解:
(1)∵四边形ABCD是矩形,
∴∠ABC=90°,且∠ACB=30°,
∴AC=2AB,
设AB=x,则AC=2x,在Rt△ABCD中,由勾股定理可得x2+32=(2x)2,解得x=$\sqrt{3}$或x=-$\sqrt{3}$(舍去),
∴AB=$\sqrt{3}$,AC=2$\sqrt{3}$;
(2)四边形BOCE是菱形,理由如下:
∵BE∥AC,CE∥BD,
∴四边形BOCE是平行四边形,
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴BO=CO,
∴四边形BOCE是菱形.
点评 本题主要考查矩形的性质和菱形的判定,掌握矩形的四个角都是直角、对角线相等且平分是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
11.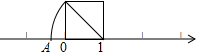 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )| A. | -$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | -1-$\sqrt{2}$ | D. | -1+$\sqrt{2}$ |

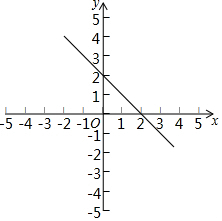 在平面直角坐标系中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C.
在平面直角坐标系中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C.