题目内容
7.直角三角形两直角边长分别为3和4,那么它的外接圆的直径是5.分析 根据直角三角形外接圆的圆心是斜边的中点,由勾股定理求得斜边,即可得出答案.
解答  解:如图,∵AC=4,BC=3,∠C=90°,
解:如图,∵AC=4,BC=3,∠C=90°,
∴AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴外接圆直径=斜边长=5.
故答案为:5.
点评 本题考查了三角形的外接圆以及外心、勾股定理;熟记直角三角形的外心是斜边的中点,斜边长是直径是解决问题的突破口.

练习册系列答案
相关题目
15.下列命题正确的是( )
| A. | 若两条弧的长相等,则这两条弧是等弧 | |
| B. | 两条弧的长相等,它们所对的圆心角也相等 | |
| C. | 两个相等的圆心角所对的两条弧的长相等 | |
| D. | 如果两个圆的周长相等,那么它们的半径也相等 |
16.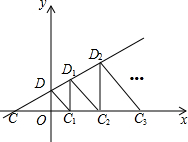 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )| A. | $\frac{4025}{2014}$ | B. | $\frac{{3}^{2012}}{{3}^{2013}}$ | C. | $\frac{{3}^{2013}}{{3}^{2012}}$ | D. | ($\frac{3}{2}$)2013 |
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为3.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为3.
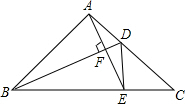 如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.
如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.