题目内容
3.(1)解不等式组:$\left\{\begin{array}{l}{5x-3>3(x-2)}\\{\frac{2}{3}-x>-\frac{1}{3}x}\end{array}\right.$(2)因式分解:(a2+1)2-4a2
(3)解方程:$\frac{x}{x-2}$+$\frac{2}{{x}^{2}-4}$=1.
分析 (1)分别求出不等式组中两不等式的解集,找出解集的公共部分即可;
(2)原式利用平方差公式及完全平方公式分解即可;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)$\left\{\begin{array}{l}{5x-3>3(x-2)①}\\{\frac{2}{3}-x>-\frac{1}{3}x②}\end{array}\right.$,
由①得:x>-$\frac{3}{2}$,
由②得:x<1,
则不等式组的解集为-$\frac{3}{2}$<x<1;
(2)原式=(a2+1+2a)(a2+1-2a)=(a+1)2(a-1)2;
(3)去分母得:x2+2x+2=x2-4,
解得:x=-3,
经检验x=-3是分式方程的解.
点评 此题考查了解分式方程,因式分解-运用公式法,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.在平面直角坐标系中,已知点A(0,3),B(1,0),C(0,-2),D(3,4),求过其中三个点的抛物线的顶点坐标是( )
| A. | (-$\frac{7}{5}$,$\frac{4}{15}$) | B. | ($\frac{7}{5}$,-$\frac{4}{15}$) | C. | (-$\frac{7}{5}$,-$\frac{4}{15}$) | D. | ($\frac{7}{5}$,$\frac{4}{15}$) |
 如图,边长为2的菱形ABCD中,∠BAD=60°,现有∠BFE=30°的三角板△BEF,将△BEF绕B旋转得△BE′F′,BE′,BF′所在直线分别交线段AC于点M,N,若点C关于直线BE′的对称点为C′,当C′N⊥AC时,AN的长为$\sqrt{3}$-1.
如图,边长为2的菱形ABCD中,∠BAD=60°,现有∠BFE=30°的三角板△BEF,将△BEF绕B旋转得△BE′F′,BE′,BF′所在直线分别交线段AC于点M,N,若点C关于直线BE′的对称点为C′,当C′N⊥AC时,AN的长为$\sqrt{3}$-1.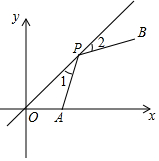 如图,在平面直角坐标系中,点A(2,0),点B(6,4),点P是直线y=x上一点,若∠1=∠2,则点P的坐标是(3,3).
如图,在平面直角坐标系中,点A(2,0),点B(6,4),点P是直线y=x上一点,若∠1=∠2,则点P的坐标是(3,3).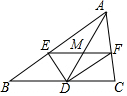 如图,在△ABC中,D是BC上的一点,DE平分∠ADB,DF平分∠ADC,且EF∥BC,若EF交AD于M,EF=18,则DM=9.
如图,在△ABC中,D是BC上的一点,DE平分∠ADB,DF平分∠ADC,且EF∥BC,若EF交AD于M,EF=18,则DM=9.