题目内容
11.我们规定,若关于x的一元一次方程ax=b的解为b-a,则称该方程为“差解方程”,例如:2x=4的解为2,且2=4-2,则该方程2x=4是差解方程.请根据上述规定解答下列问题:
(1)判断3x=4.5是否是差解方程;
(2)若关于x的一元一次方程5x=m+1是差解方程,求m的值.
分析 (1)解方程,并计算对应b-a的值与方程的解恰好相等,所以是差解方程;
(2)解方程,根据差解方程的定义列式,解出即可.
解答 解:(1)∵3x=4.5,
∴x=1.5,
∵4.5-3=1.5,
∴3x=4.5是差解方程;
(2)5x=m+1,
x=$\frac{m+1}{5}$,
∵关于x的一元一次方程5x=m+1是差解方程,
∴m+1-5=$\frac{m+1}{5}$,
解得:m=$\frac{21}{4}$.
点评 本题考查了一元一次方程的解与新定义:差解方程,解好本题是做好两件事:①熟练掌握一元一次方程的解法;②明确差解方程的定义,即b-a=方程的解.

练习册系列答案
相关题目
16.下列方程中是一元一次方程的是( )
| A. | x2-2x=4 | B. | x+2=0 | C. | x+3y=7 | D. | x-1=$\frac{1}{x}$ |
20.下列运算正确的是( )
| A. | -22=4 | B. | (3$\frac{1}{2}$)3=-8$\frac{1}{27}$ | C. | (-$\frac{1}{2}$)3=-$\frac{1}{8}$ | D. | (-2)3=-6 |
16. 设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:
设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:
(1)在如图的坐标系中,用描点法画出相应函数的图线;
(2)求y关于x的函数解析式;
(3)如果三角形BC边的长不小于8cm,求高线AD范围.
 设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:
设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 6 | 2.9 | 2.1 | 1.5 | 1.2 | 1 |
(2)求y关于x的函数解析式;
(3)如果三角形BC边的长不小于8cm,求高线AD范围.
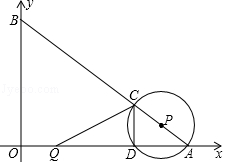 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.