题目内容
8.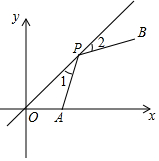 如图,在平面直角坐标系中,点A(2,0),点B(6,4),点P是直线y=x上一点,若∠1=∠2,则点P的坐标是(3,3).
如图,在平面直角坐标系中,点A(2,0),点B(6,4),点P是直线y=x上一点,若∠1=∠2,则点P的坐标是(3,3).
分析 过B作BN⊥x轴于N,过P作PM⊥x轴于M,PC⊥BN于C,设P的坐标为(a,a),求出△MPA∽△CPB,得出比例式,即可求出a.
解答 解:
过B作BN⊥x轴于N,过P作PM⊥x轴于M,PC⊥BN于C,
则∠PCB=∠PMA=90°,∠PCN=∠CNM=∠PMN=90°,
所以四边形MNCP是矩形,
∵四边形MNCP是矩形,
∴PC=MN,PM=CN,∠CPM=90°,PC∥MN,
∵∠1=∠2,P在直线y=x上,
∴∠2+∠BPC=∠POA=45°=∠1+∠APM,
∴∠BPC=∠MPA,
设P的坐标为(a,a),
∵点A(2,0),点B(6,4),
∴PM=a,AM=a-2,PC=6-a,BC=4-a,
∵∠BPC=∠MPA,∠PCB=∠PMA=90°,
∴△MPA∽△CPB,
∴$\frac{PM}{PC}$=$\frac{AM}{BC}$,
∴$\frac{a}{6-a}$=$\frac{a-2}{4-a}$,
解得:a=3,
即P的坐标为(3,3),
故答案为:(3,3).
点评 本题考查了一次函数图象上点的坐标,相似三角形的性质和判定,矩形的性质和判定等知识点,能求出△MPA∽△CPB是解此题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
16.下列方程中是一元一次方程的是( )
| A. | x2-2x=4 | B. | x+2=0 | C. | x+3y=7 | D. | x-1=$\frac{1}{x}$ |
20.下列运算正确的是( )
| A. | -22=4 | B. | (3$\frac{1}{2}$)3=-8$\frac{1}{27}$ | C. | (-$\frac{1}{2}$)3=-$\frac{1}{8}$ | D. | (-2)3=-6 |
 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边AC上一点O为圆心,OA为半径作圆,恰好经过边BC的中点D,并与边AC相交于另一点F.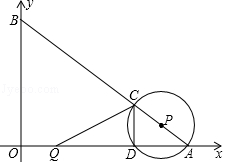 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.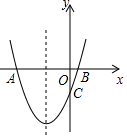 如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).
如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).