题目内容
3. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则比较下列大小:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则比较下列大小:①abc<0;②4a+2b+c>0;③2c<3b;④a+b≤n(an+b).
分析 根据开口方向、对称轴、抛物线与y轴的交点,确定a、b、c的符号,根据对称轴和图象确定y>0或y<0时,x的范围,确定代数式的符号.
解答 解:①开口向下,∴a<0,对称轴在y轴的右侧,b>0,抛物线与y轴交于正半轴,c>0,∴abc<0;
②由对称轴和图象可知,当x=2时,y>0,4a+2b+c>0;
③-$\frac{b}{2a}$=1,a=-$\frac{b}{2}$,
a-b+c<0,∴2c<3b;
x=1时,y有最小值a+b+c,
a+b+c≤an2+bn+c,∴a+b≤n(an+b)
故答案为:<;>;<;≤.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
相关题目
15.二次函数y=$\frac{1}{2}$x2-2的最小值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 如图,AD=4.8厘米,点C是线段AB的中点,点D是线段CB的中点,则AB=6.4厘米.
如图,AD=4.8厘米,点C是线段AB的中点,点D是线段CB的中点,则AB=6.4厘米.



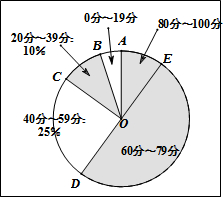 如图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
如图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.