题目内容
18.等腰三角形△ABC底角的余弦值是$\frac{3}{4}$,一边长为12,则等腰三角形的面积为$27\sqrt{7}$或$12\sqrt{7}$.分析 分两种情况:①一边长腰为12,根据等腰三角形△ABC底角的余弦值是$\frac{3}{4}$,以及等腰三角形的性质得到底和高,再根据三角形面积公式即可求解;②一边长底为12,根据等腰三角形△ABC底角的余弦值是$\frac{3}{4}$,以及等腰三角形的性质得到高,再根据三角形面积公式即可求解.
解答 解:①如图1:
一边长腰AB为12,在△ABC中,底角∠B的余弦值是$\frac{3}{4}$,
则BD=12×$\frac{3}{4}$=9,AD=$\sqrt{1{2}^{2}-{9}^{2}}$=3$\sqrt{7}$,
则BC=2BD=18,
则等腰三角形的面积为18×3$\sqrt{7}$÷2=$27\sqrt{7}$;
②如图2:
一边长底BC为12,
则BD=6,
在△ABC中,底角∠B的余弦值是$\frac{3}{4}$,
则AD=6÷$\frac{3}{4}$=8,AD=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$,
则等腰三角形的面积为12×2$\sqrt{7}$÷2=$12\sqrt{7}$.
故等腰三角形的面积为$27\sqrt{7}$或$12\sqrt{7}$.
故答案为:$27\sqrt{7}$或$12\sqrt{7}$.
点评 本题考查了解直角三角形,解题的关键是注意作底边上的高,并且利用勾股定理,要考虑两种情况.

练习册系列答案
相关题目
6.若线段AB=3cm,BC=5cm,则线段AC的长为( )
| A. | 2cm | B. | 8cm | C. | 2cm或8cm | D. | 不能确定 |
7.将抛物线y=x2平移得到抛物线y=x2-4,下列平移正确的是( )
| A. | 向上平移4个单位 | B. | 向下平移4个单位 | C. | 向左平移4个单位 | D. | 向右平移4个单位 |
8.若x,y满足|x-3|+$\sqrt{y-6}$=0,则以x,y的值为两边长的等腰三角形的周长为( )
| A. | 12 | B. | 14 | C. | 15 | D. | 12或15 |
 如图,已知AC=3AB,BC=12,点D 是线段AC的中点,求BD的长度.
如图,已知AC=3AB,BC=12,点D 是线段AC的中点,求BD的长度. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则比较下列大小:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则比较下列大小: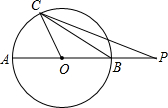 如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.
如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.