题目内容
6.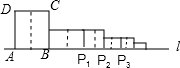 如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°得到BP1为边的新矩形,我们称之为第1次操作,沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以P1为中心顺时针旋转90°,得到P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2015的长是$\frac{{2}^{1008}-1}{{2}^{1006}}$.
如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°得到BP1为边的新矩形,我们称之为第1次操作,沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以P1为中心顺时针旋转90°,得到P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2015的长是$\frac{{2}^{1008}-1}{{2}^{1006}}$.
分析 根据旋转的性质和矩形的性质易得AB=1,BP1=1,P1P2=$\frac{1}{2}$,P2P3=$\frac{1}{2}$,P3P4=($\frac{1}{2}$)2,P4P5=($\frac{1}{2}$)2,P5P6=($\frac{1}{2}$)3,P6P7=($\frac{1}{2}$)3,根据P的脚标数与$\frac{1}{2}$的指数的关系易得P2013P2014=($\frac{1}{2}$)1007,P2014P2015=($\frac{1}{2}$)1007,所以AP2015=3+$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006,接着利用方程的思想计算出$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006=1-($\frac{1}{2}$)1006,则AP2015=4-($\frac{1}{2}$)1006.
解答 解:AB=1,BP1=1,
P1P2=$\frac{1}{2}$,P2P3=$\frac{1}{2}$,
P3P4=($\frac{1}{2}$)2,P4P5=($\frac{1}{2}$)2,
P5P6=($\frac{1}{2}$)3,P6P7=($\frac{1}{2}$)3,
…
P2013P2014=($\frac{1}{2}$)1007,P2014P2015=($\frac{1}{2}$)1007,
所以AP2015=2×1+2[$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1007]=3+$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006,
设$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1006=S,
则1+$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)1005=2S,
所以S=1-($\frac{1}{2}$)1006,
所以AP2015=3+1-($\frac{1}{2}$)1006=$\frac{{2}^{1008}-1}{{2}^{1006}}$.
故答案为=$\frac{{2}^{1008}-1}{{2}^{1006}}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查通过从特殊到一般解决规律型问题.

| 6,8,10 | 8,15,17 | 10,24,26 | … | 20,b,c |
| 62+82=102 | 82+152=172 | 102+242=262 | … | 202+b2=c2 |
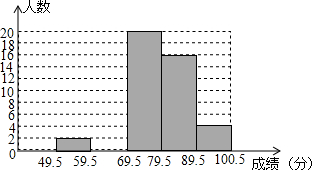 我校艺术节期间,开展了“巴蜀好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图表提供的信息,解答下列问题:
我校艺术节期间,开展了“巴蜀好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图表提供的信息,解答下列问题:| 分组 | 74.5~79.5 | 79.5~84.5 | 84.5~89.5 | 89.5~94.5 | 94.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
(2)补全频数分布直方图;
(3)初赛成绩在94.5-100.5分的四位同学恰好是初一、初二、高一、高二年级各一位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,请你用列表法或画树状图的方法求出所选两位同学恰好是一名初中和一名高中同学的概率.
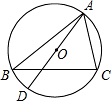 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
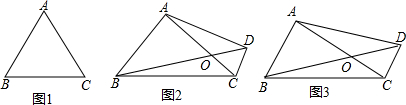
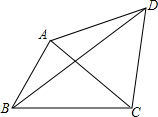 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,△ACD是等边三角形,连接BD,则线段BD的长为$\sqrt{19}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,△ACD是等边三角形,连接BD,则线段BD的长为$\sqrt{19}$.