题目内容
15.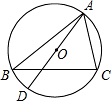 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 连接CD,根据正弦的概念求出sinD,根据圆周角定理证明∠B=∠D,得到答案.
解答  解:连接CD,
解:连接CD,
∵⊙O的半径为$\frac{3}{2}$,∴直径AD=3,
sinD=$\frac{AC}{AD}$=$\frac{2}{3}$,
∵∠B=∠D,
∴sinB=$\frac{2}{3}$,
故选:A.
点评 本题考查的是圆周角定理和锐角三角函数的知识,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等和锐角三角函数的概念是解题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
10.已知两圆的半径是4和5,圆心距满足不等式组$\left\{\begin{array}{l}{x+2>\frac{x+5}{2}}\\{5x-4<2x+23}\end{array}\right.$,则两圆的位置关系是( )
| A. | 相交 | B. | 外切 | C. | 内切 | D. | 外离 |
4.要调查姜堰城区八年级5000名学生了解“溱潼会船节”的情况,下列调查方式最合适的是( )
| A. | 在某校八年级选取100名女生 | |
| B. | 在某校八年级选取100名男生 | |
| C. | 在某校八年级选取100名学生 | |
| D. | 在城区5000名八年级学生中随机选取100名学生 |
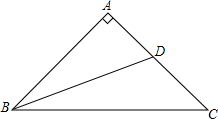 如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC.
如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC.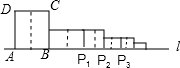 如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°得到BP1为边的新矩形,我们称之为第1次操作,沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以P1为中心顺时针旋转90°,得到P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2015的长是$\frac{{2}^{1008}-1}{{2}^{1006}}$.
如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°得到BP1为边的新矩形,我们称之为第1次操作,沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以P1为中心顺时针旋转90°,得到P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2015的长是$\frac{{2}^{1008}-1}{{2}^{1006}}$.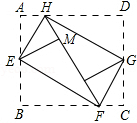 如图,将长方形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的长方形EFGH.若AE=3,FH=7,则原长方形的面积为42.
如图,将长方形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的长方形EFGH.若AE=3,FH=7,则原长方形的面积为42.