题目内容
在△ABC中,∠BAC=90°,AB=5,BC=13,AD是BC边上的高,AD=4,求:
(1)CD和sinC;
(2)如果∠BAC<90°呢?
(1)CD和sinC;
(2)如果∠BAC<90°呢?
考点:解直角三角形
专题:计算题
分析:(1)画出相应图形,如图所示,由AB与BC的长,利用勾股定理求出AC的长,进而求出CD与sinC的长;
(2)若∠BAC<90°,在直角三角形ABD中,由AB与AD的长,利用勾股定理求出BD的长,由BC-BD求出CD的长,在直角三角形ACD中,利用勾股定理求出AC的长,利用锐角三角函数定义求出sinC的值即可.
(2)若∠BAC<90°,在直角三角形ABD中,由AB与AD的长,利用勾股定理求出BD的长,由BC-BD求出CD的长,在直角三角形ACD中,利用勾股定理求出AC的长,利用锐角三角函数定义求出sinC的值即可.
解答: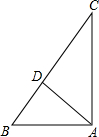 解:(1)如图所示:
解:(1)如图所示:
∵∠BAC=90°,AB=5,BC=13,
∴根据勾股定理得:AC=
=12,
∵cosC=
=
,
∴CD=ACcosC=12×
=
;sinC=
=
;
(2)若∠BAC<90°,
在Rt△ABD中,AB=5,AD=4,
根据勾股定理得:BD=
=3,
则CD=13-3=10;
在Rt△ADC中,AD=4,CD=10,
根据勾股定理得:AC=
=
=2
,
则sinC=
=
=
.
 解:(1)如图所示:
解:(1)如图所示:∵∠BAC=90°,AB=5,BC=13,
∴根据勾股定理得:AC=
| 132-52 |
∵cosC=
| AC |
| BC |
| 12 |
| 13 |
∴CD=ACcosC=12×
| 12 |
| 13 |
| 144 |
| 13 |
| AB |
| BC |
| 5 |
| 13 |
(2)若∠BAC<90°,
在Rt△ABD中,AB=5,AD=4,
根据勾股定理得:BD=
| 52-42 |
则CD=13-3=10;
在Rt△ADC中,AD=4,CD=10,
根据勾股定理得:AC=
| 42+102 |
| 116 |
| 29 |
则sinC=
| AD |
| AC |
| 4 | ||
2
|
2
| ||
| 29 |
点评:此题属于解直角三角形题型,涉及的知识有:勾股定理,锐角三角函数定义,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
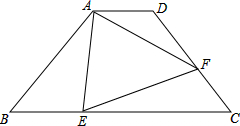 如图,等腰梯形ABCD中,AD∥BC,AD=2,AB=5,BC=8,点E在BC上,点F在CD上,且满足∠AEF=∠B,AF=EF,求BE的长.
如图,等腰梯形ABCD中,AD∥BC,AD=2,AB=5,BC=8,点E在BC上,点F在CD上,且满足∠AEF=∠B,AF=EF,求BE的长. 如图,已知线段AB.
如图,已知线段AB.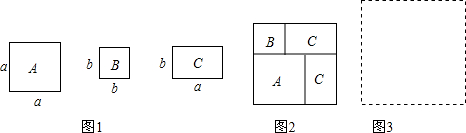
 小王在一块一边靠墙,长为8米,宽为5米的矩形小花园周围栽种了一种花作修饰,如图所示,这块花园的边框宽为30厘米,内外边框所圈的两个矩形相似吗?为什么?
小王在一块一边靠墙,长为8米,宽为5米的矩形小花园周围栽种了一种花作修饰,如图所示,这块花园的边框宽为30厘米,内外边框所圈的两个矩形相似吗?为什么?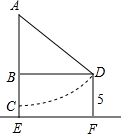 华夏古诗词源远流长,有许多古诗词与勾股定理有紧密联系,下面是明朝大数学家程大位所著的《直指算法统宗》里的一道题:
华夏古诗词源远流长,有许多古诗词与勾股定理有紧密联系,下面是明朝大数学家程大位所著的《直指算法统宗》里的一道题: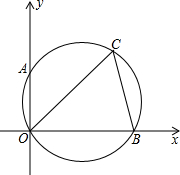 如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标.
如图,在平面直角坐标系中,△OBC的外接圆交y轴于点A(0,2),∠OCB=60°,∠COB=45°.求点C的坐标.