题目内容
 小王在一块一边靠墙,长为8米,宽为5米的矩形小花园周围栽种了一种花作修饰,如图所示,这块花园的边框宽为30厘米,内外边框所圈的两个矩形相似吗?为什么?
小王在一块一边靠墙,长为8米,宽为5米的矩形小花园周围栽种了一种花作修饰,如图所示,这块花园的边框宽为30厘米,内外边框所圈的两个矩形相似吗?为什么?考点:相似多边形的性质
专题:应用题
分析:先求出内外边框所围成的矩形的长与宽,然后求出两个矩形的长与宽的比,再根据相似矩形的判定方法解答.
解答:解:不相似.
理由:∵内边框内缘所围成的矩形的长=8-0.3×2=7.4米,
宽=5-0.3=4.7米,
∴长与宽的比为:
=
,原矩形的长与宽之比=
∵
≠
,
∴内外边框所围成的两个矩形不相似.
理由:∵内边框内缘所围成的矩形的长=8-0.3×2=7.4米,
宽=5-0.3=4.7米,
∴长与宽的比为:
| 7.4 |
| 4.7 |
| 74 |
| 47 |
| 8 |
| 5 |
∵
| 74 |
| 47 |
| 8 |
| 5 |
∴内外边框所围成的两个矩形不相似.
点评:本题考查了相似多边形的对应边成比例的性质,求出两个矩形的长于宽的比是解题的关键.

练习册系列答案
相关题目
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
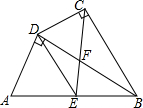 如图,四边形ABCD中,∠ADB=∠DCB=90°,BD平分∠ABC,点E为AB中点.
如图,四边形ABCD中,∠ADB=∠DCB=90°,BD平分∠ABC,点E为AB中点. 二次函数y=ax2+bx+c的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,求k的取值范围.
二次函数y=ax2+bx+c的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,求k的取值范围. 如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB.
如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB. 已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.
已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC. 如图,直线EF,CD相交于点O,∠AOB=90°,且OD平分∠AOF,∠BOE=2∠AOE,求∠EOD的度数.
如图,直线EF,CD相交于点O,∠AOB=90°,且OD平分∠AOF,∠BOE=2∠AOE,求∠EOD的度数.