题目内容
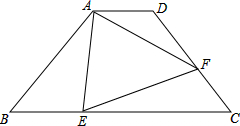 如图,等腰梯形ABCD中,AD∥BC,AD=2,AB=5,BC=8,点E在BC上,点F在CD上,且满足∠AEF=∠B,AF=EF,求BE的长.
如图,等腰梯形ABCD中,AD∥BC,AD=2,AB=5,BC=8,点E在BC上,点F在CD上,且满足∠AEF=∠B,AF=EF,求BE的长.考点:等腰梯形的性质,相似三角形的判定与性质
专题:
分析:由等腰梯形的性质得,∠B=∠C,由外角的性质得,∠BAE=∠FEC,则△ABE∽△FEC,分别过A、D作AG、DH垂直于BC分别交于点G、H,则cos∠B=
,因为AF=FE,则有cos∠AEF=
=cos∠B=
,即
=
,
根据△ABE∽△ECF,得出
=
,即
=
,解得x=
.
| 3 |
| 5 |
| ||
| EF |
| 3 |
| 5 |
| AE |
| EF |
| 6 |
| 5 |
根据△ABE∽△ECF,得出
| AE |
| EF |
| AB |
| EC |
| 5 |
| 8-x |
| 6 |
| 5 |
| 23 |
| 6 |
解答: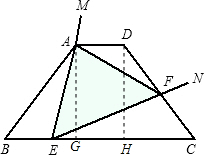 解:∵AB=DC=5,
解:∵AB=DC=5,
∴∠B=∠C
而∠AEC=∠B+∠BAE=∠AEF+∠FEC
∵∠AEF=∠B,
∴∠BAE=∠FEC
∴△ABE∽△ECF
分别过A、D作AG、DH垂直于BC分别交于点G、H可推得cos∠B=
=
,
∵AF=FE,
∴cos∠AEF=
=cos∠B=
,
∴
=
,
∵△ABE∽△ECF,
∴
=
,即
=
,解得x=
,
∴BE的长为
.
 解:∵AB=DC=5,
解:∵AB=DC=5,∴∠B=∠C
而∠AEC=∠B+∠BAE=∠AEF+∠FEC
∵∠AEF=∠B,
∴∠BAE=∠FEC
∴△ABE∽△ECF
分别过A、D作AG、DH垂直于BC分别交于点G、H可推得cos∠B=
| BG |
| AB |
| 3 |
| 5 |
∵AF=FE,
∴cos∠AEF=
| ||
| EF |
| 3 |
| 5 |
∴
| AE |
| EF |
| 6 |
| 5 |
∵△ABE∽△ECF,
∴
| AE |
| EF |
| AB |
| EC |
| 5 |
| 8-x |
| 6 |
| 5 |
| 23 |
| 6 |
∴BE的长为
| 23 |
| 6 |
点评:本题考查了相似三角形的判定和性质、解直角三角形、等腰三角形的性质.

练习册系列答案
相关题目
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
截止到4月25日,雅安三个重灾县的直接经济损失已经达到了上年GDP总和的21倍,已知上年GDP总和约为80亿元,则三个重灾县的直接经济损失用科学记数法表示约为( )
| A、1680亿元 |
| B、1.68×1011元 |
| C、1.68×1012元 |
| D、0.168×1012元 |
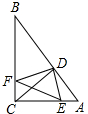 已知,在Rt△ABC中,∠BCA=90°,CD是斜边AB边上的高,点E、F分别是AC、BC边上的点,连接DE、DF、EF,且∠EDF=90°.
已知,在Rt△ABC中,∠BCA=90°,CD是斜边AB边上的高,点E、F分别是AC、BC边上的点,连接DE、DF、EF,且∠EDF=90°.