题目内容
17．
如图，符合图象的解析式是④．（填序号）①y=$\frac{2}{x}$ ②y=$\frac{-2}{x}$ ③y=$\frac{2}{x}$和y=$\frac{-2}{x}$ ④y=$\frac{2}{|x|}$．
分析 根据图象为双曲线，并且在第一和第二象限，可得出图象为④．
解答 解：∵双曲线在第一和第二象限，
∴y＞0，
∴应选④，
故答案为④．
点评 本题考查了反比例函数的图象，反比例函数y=$\frac{k}{x}$的图象是双曲线，当k＞0时，它的两个分支分别位于第一、三象限；当k＜0时，它的两个分支分别位于第二、四象限．
练习册系列答案
天天练口算系列答案
相关题目
7．已知两条线段的长分别为$\sqrt{2}$cm、$\sqrt{3}$cm，那么能与它们组成直角三角形的第三条线段是（ ）
| A． | 1cm | B． | $\sqrt{5}$cm | C． | 5cm | D． | 1cm或$\sqrt{5}$cm |
8．下列代数式中，全是单项式的一组是（ ）
| A． | 2xy，$\frac{x-1}{3}$，a | B． | $\frac{x}{π}$，-2，$\frac{{a}^{2}b}{3}$ | C． | $\frac{1}{x}$，x2y，-m | D． | x+y，xyz，2a2 |
教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）之间的关系为y=-$\frac{1}{10}$（x-4）2+3，由此可知铅球推出的距离是（4+$\sqrt{30}$）m．
9．
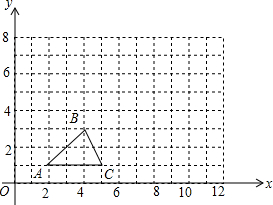已知△ABC的三个顶点坐标如表：
（1）将下表补充完整，并在直角坐标系中，画出△A′B′C′；
（2）观察△ABC与△A′B′C′，写出有关这两个三角形关系的一个正确结论．
（3）求直线BC′的解析式．
已知△ABC的三个顶点坐标如表：（1）将下表补充完整，并在直角坐标系中，画出△A′B′C′；
（2）观察△ABC与△A′B′C′，写出有关这两个三角形关系的一个正确结论．
（3）求直线BC′的解析式．
| （x，y） | （2x，2y） |
| A（2，1） | A′（4，2） |
| B（4，3） | B′（8，6） |
| C（5，1） | C′（10，2） |
