题目内容
5．（1）解不等式：3x-1＜2x+4（2）不等式组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{x}{3}＞-1}\\{2（x-3）-3（x-2）＞-6}\end{array}\right.$并将其解集在数轴上表示出来．
分析 （1）移项、合并同类项可得解集；
（2）分别求出每个不等式解集，找到其公共部分即可的不等式组解集，并表示在数轴上．
解答 解：（1）移项，得：3x-2x＜4+1，
合并同类项，得：x＜5；
（2）解不等式组：$\left\{\begin{array}{l}{\frac{x}{2}-\frac{x}{3}＞-1}&{①}\\{2（x-3）-3（x-2）＞-6}&{②}\end{array}\right.$，
解不等式①，得：x＞-6，
解不等式②，得：x＜6，
∴不等式组的解集为：-6＜x＜6，
表示在数轴上如下所示：
点评 本题主要考查解一元一次不等式、不等式组的能力，严格遵循解不等式的基本步骤是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，△ABC中，D是BC的中点，CE⊥AD于E．BF⊥AD交AD的延长线于F，求证：BF=CE．
16．某教室的开关控制板上有四个外形完全相同的开关，其中两个分别控制A、B两盏电灯，另两个分别控制C、D两个吊扇．已知电灯、吊扇均正常，且处于不工作状态，开关与电灯、电扇的对应关系未知．若四个开关均正常，则任意按下一个开关，正好一盏灯亮的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | .1 |
13．完成某项工程，甲独做需a天，乙独做需b天，甲乙两人合作完成这项工程的一半需要的天数是（ ）
| A． | $\frac{a+b}{ab}$ | B． | $\frac{ab}{2（a+b）}$ | C． | $\frac{a+b}{2ab}$ | D． | $\frac{ab}{a+b}$ |
如图，在四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=4$\sqrt{2}$，CD=2$\sqrt{2}$，点P在四边形ABCD的边上，若点P到BD的距离为3，则点P的个数为（ ）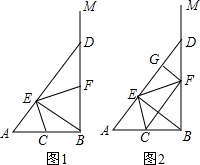
如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B重合），连结AD，作BE⊥AD，垂足为E，连结CE，过点E作EF⊥CE，交BD于F．
如图，符合图象的解析式是④．（填序号）
如图，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点，已知B点的坐标为（-1，1），将△ABC绕着点C顺时针旋转90°，则点A的对应点的坐标为（5，-1）．