题目内容
2. 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{10}$(x-4)2+3,由此可知铅球推出的距离是(4+$\sqrt{30}$)m.
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{10}$(x-4)2+3,由此可知铅球推出的距离是(4+$\sqrt{30}$)m.
分析 根据铅球落地时,高度y=0,实际问题可理解为当y=0时,求x的值即可.
解答 解:令函数式y=-$\frac{1}{10}$(x-4)2+3中,y=0,
0=-$\frac{1}{10}$(x-4)2+3,
解得x1=4+$\sqrt{30}$,x2=4-$\sqrt{30}$(舍去),
即铅球推出的距离是(4+$\sqrt{30}$)m.
故答案为:(4+$\sqrt{30}$).
点评 本题考查了二次函数的应用中函数式中自变量与函数表达的实际意义,需要结合题意,取函数或自变量的特殊值列方程求解是解题关键.

练习册系列答案
相关题目
13.完成某项工程,甲独做需a天,乙独做需b天,甲乙两人合作完成这项工程的一半需要的天数是( )
| A. | $\frac{a+b}{ab}$ | B. | $\frac{ab}{2(a+b)}$ | C. | $\frac{a+b}{2ab}$ | D. | $\frac{ab}{a+b}$ |
11.在下列各多项式乘法中不能用平方差公式的是( )
| A. | (m+n)(-m+n) | B. | (x3-y3)(x3+y3) | C. | (-a-b)(a+b) | D. | ( $\frac{1}{3}$a-b)( $\frac{1}{3}$a+b) |
12.等式$\frac{1-3x}{\frac{2}{3}}$-3=2x的下列变形属于等式基本性质2变形的是( )
| A. | $\frac{1-3x}{2}$-3=2x+3 | B. | $\frac{3(1-3x)}{2}$-3=2x | C. | 3(1-3x)-6=4x | D. | 3(1-3x)-4x=6 |
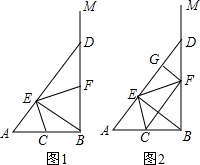 如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合),连结AD,作BE⊥AD,垂足为E,连结CE,过点E作EF⊥CE,交BD于F.
如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合),连结AD,作BE⊥AD,垂足为E,连结CE,过点E作EF⊥CE,交BD于F. 如图,符合图象的解析式是④.(填序号)
如图,符合图象的解析式是④.(填序号) 一副三角板,如图所示叠放在一起,则图中∠α的度数是75°.
一副三角板,如图所示叠放在一起,则图中∠α的度数是75°. 如图,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B点的坐标为(-1,1),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1).
如图,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B点的坐标为(-1,1),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1).