题目内容
11.在锐角△ABC中,AB=4$\sqrt{2}$,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)点E是AB中点,点P是边AC上的动点,点P1是点P的对应点,求线段EP1最大值和最小值.
分析 (1)如图1,根据旋转的性质得∠A1C1B=∠ACB=45°,BC=BC1,则根据等腰三角形的性质得∠CC1B=∠C1CB=45°,所以∠CC1A1=∠CC1B+∠A1C1B=90°;
(2)如图2(a),过点B作BD⊥AC,D为垂足,则点D在线段AC上,在Rt△BCD中,利用正弦定义可计算出BD=$\frac{5\sqrt{2}}{2}$,则BP与AC垂直,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值=EP1=BP1-BE=$\frac{5\sqrt{2}}{2}$-2;如图2(b),当△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值=EP1=BC+BE=7.
解答 解:(1)如图1,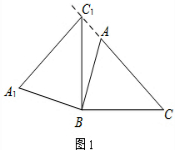
∵△ABC绕点B按逆时针方向旋转,得到△A1BC1,点C1在线段CA的延长线上,
∴∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°;
(2)如图2(a),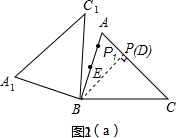
过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=5×$\frac{\sqrt{2}}{2}$=$\frac{5\sqrt{2}}{2}$,
当P在AC上运动,BP与AC垂直,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值=EP1=BP1-BE=BD-BE=$\frac{5\sqrt{2}}{2}$-2;
如图2(b),当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值=EP1=BC+BE=2+5=7.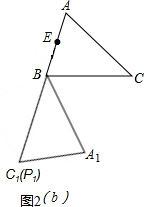
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

 53随堂测系列答案
53随堂测系列答案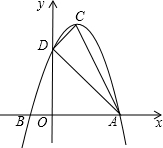 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D. 若a、b在数轴上的表示如图:则化简2|a|-|b|+|a+b|-|a-b|的结果是b.
若a、b在数轴上的表示如图:则化简2|a|-|b|+|a+b|-|a-b|的结果是b. 如图,已知直线y=kx-3经过点M,求此直线的函数关系式,并求与x轴、y轴的交点坐标.
如图,已知直线y=kx-3经过点M,求此直线的函数关系式,并求与x轴、y轴的交点坐标.