题目内容
3. 如图,在△ABC中,AB=3,AC=4,BC=5,P为BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为2.4.
如图,在△ABC中,AB=3,AC=4,BC=5,P为BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为2.4.
分析 根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
解答 解:∵在△ABC中,AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
即∠BAC=90°.
又∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF=AP.
因为AP的最小值即为直角三角形ABC斜边上的高,即2.4,
∴EF的最小值为2.4,
故答案为:2.4.
点评 此题综合运用了勾股定理的逆定理、矩形的判定及性质、直角三角形的性质,要能够把要求的线段的最小值转换为便于分析其最小值的线段.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
13.函数y=-x2具有性质( )
| A. | 无论x为何值,y的值总是负值 | B. | 当x的值增加时,y随着减小 | ||
| C. | 它的图象关于y轴对称 | D. | 它的图象在第三、四象限 |
14. 如图,在△ABC中,AB=AC,BC=6,AD=4,E,F是中线AD上的两点,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC,BC=6,AD=4,E,F是中线AD上的两点,则图中阴影部分的面积是( )
 如图,在△ABC中,AB=AC,BC=6,AD=4,E,F是中线AD上的两点,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC,BC=6,AD=4,E,F是中线AD上的两点,则图中阴影部分的面积是( )| A. | 6 | B. | 12 | C. | 24 | D. | 30 |
11.下列含有字母的式子,符合书写规范要求的是( )
| A. | -1a | B. | $5\frac{1}{2}b$ | C. | 0.5xy | D. | (x+y)+z |
15.要了解全校2000名学生课外作业负担情况,你认为以下抽样方法中比较合理的是( )
| A. | 调查全体男生 | B. | 调查全体女生 | ||
| C. | 调查七年级全体学生 | D. | 调查各年级中的部分学生 |
13.若⊙O的半径为r,且r<OA,则点A在( )
| A. | ⊙O内 | B. | ⊙O外 | C. | ⊙O上 | D. | 不能确定 |
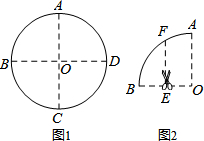 如图1,将半径为2的圆形纸片沿圆的两条互相垂直的直径AC、BD两次折叠后,得到如图2所示的扇形OAB,然后再沿OB的中垂线EF将扇形OAB剪成左右两部分,则∠OEF=90°;右边部分经过两次展开并压平后所得的图形的周长为$\frac{4π}{3}$+4$\sqrt{3}$.
如图1,将半径为2的圆形纸片沿圆的两条互相垂直的直径AC、BD两次折叠后,得到如图2所示的扇形OAB,然后再沿OB的中垂线EF将扇形OAB剪成左右两部分,则∠OEF=90°;右边部分经过两次展开并压平后所得的图形的周长为$\frac{4π}{3}$+4$\sqrt{3}$.