Question

2．已知△ABC中，AB=6，AC=8，BC=11，任作一条直线将△ABC分成两个三角形，若其中有一个三角形是等腰三角形，则这样的直线最多有（　　）

• A． 3条
• B． 5条
• C． 7条
• D． 8条

Answer 1

分析 分别以A、B、C为等腰三角形的顶点，可画出直线，再分别以AB、AC、BC为底的等腰三角形，可画出直线，综合两种情况可求得答案．

解答 解：
分别以A、B、C为等腰三角形的顶点的等腰三角形有4个，如图1，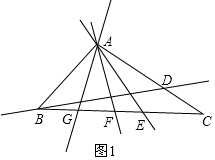

分别为△ABD、△ABE、△ABF、△ACG，
∴满足条件的直线有4条；
分别以AB、AC、BC为底的等腰三角形有3个，如图2，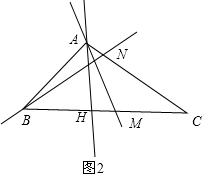

分别为△ABH、△ACM、△BCN，
∴满足条件的直线有3条，
综上可知满足条件的直线共有7条，
故选C．

点评 本题主要考查等腰三角形的性质，正确画出图形是解题的关键．