题目内容
20.在△ABC中,∠BAC=90°,∠ABC=60°,点D在直线BC上,过点D作DE⊥AC,垂足为点E,若AB=2,DE=1,则线段BD的长为2.分析 通过解直角三角形求出线段BC的长度,再根据∠BAC=90°、DE⊥AC即可得出DE∥AB,结合AB、DE的长度即可得出DE为△ABC的中位线,由此即可得出BD的长度,此题得解.
解答 解:依照题意画出图形,如图所示.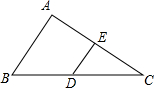
在Rt△ABC中,∠BAC=90°,∠ABC=60°,AB=2,
∴∠ACB=90°-∠ABC=30°,BC=$\frac{AB}{sin∠ACB}$=4.
∵∠BAC=90°,DE⊥AC,
∴DE∥AB,
∵DE=1,AB=2,
∴DE为△ABC的中位线,
∴BD=$\frac{1}{2}$BC=2.
故答案为:2.
点评 本题考查了含30度角的直角三角形以及中位线的性质,通过解直角三角形求出BC的长度是解题的关键.

练习册系列答案
相关题目
10.在下列各数:-(-3),(-2)×(-$\frac{1}{4}$),-|-3|,-|a|+1中,负数的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.下列含有字母的式子,符合书写规范要求的是( )
| A. | -1a | B. | $5\frac{1}{2}b$ | C. | 0.5xy | D. | (x+y)+z |
15.要了解全校2000名学生课外作业负担情况,你认为以下抽样方法中比较合理的是( )
| A. | 调查全体男生 | B. | 调查全体女生 | ||
| C. | 调查七年级全体学生 | D. | 调查各年级中的部分学生 |
9.2x+5y与4x-4y的一半的差为( )
| A. | 4x-y | B. | y-x | C. | 7y | D. | -9y |
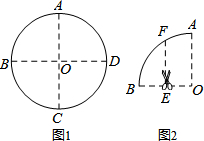 如图1,将半径为2的圆形纸片沿圆的两条互相垂直的直径AC、BD两次折叠后,得到如图2所示的扇形OAB,然后再沿OB的中垂线EF将扇形OAB剪成左右两部分,则∠OEF=90°;右边部分经过两次展开并压平后所得的图形的周长为$\frac{4π}{3}$+4$\sqrt{3}$.
如图1,将半径为2的圆形纸片沿圆的两条互相垂直的直径AC、BD两次折叠后,得到如图2所示的扇形OAB,然后再沿OB的中垂线EF将扇形OAB剪成左右两部分,则∠OEF=90°;右边部分经过两次展开并压平后所得的图形的周长为$\frac{4π}{3}$+4$\sqrt{3}$.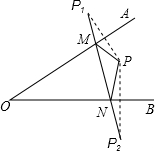 如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=22,则△PMN的周长为22.
如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=22,则△PMN的周长为22.
 如图,AD为△ABC的中线,点E为AD的中点,若△ABC面积为20cm2,则△AEC的面积为5 cm2.
如图,AD为△ABC的中线,点E为AD的中点,若△ABC面积为20cm2,则△AEC的面积为5 cm2.