题目内容
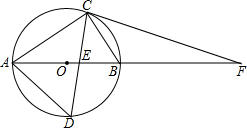 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE.(1)求AD的长.
(2)试判断直线PC与⊙O的位置关系,并说明理由.
考点:切线的判定
专题:计算题
分析:(1)先根据勾股定理计算出AB=10cm,再利用角平分线定义得∠ACD=∠BCD=45°,则利用圆周角定理得到∠BAD=∠ABD=45°,于是可判断△ABD为等腰直角三角形,然后利用AD=
AB进行计算;
(2)连结OC,如图,由PE=PC得∠PCE=∠PEC,则∠PCE=∠1+45°,利用三角形的外角性质得∠PEC=∠2+∠ACE=∠2+45°,则∠2=∠1,加上∠2=∠3,所以∠1=∠3,易得∠1+∠OCB=90°,即∠OCP=90°,所以根据切线的判定定理得到PC为⊙O的切线.
| ||
| 2 |
(2)连结OC,如图,由PE=PC得∠PCE=∠PEC,则∠PCE=∠1+45°,利用三角形的外角性质得∠PEC=∠2+∠ACE=∠2+45°,则∠2=∠1,加上∠2=∠3,所以∠1=∠3,易得∠1+∠OCB=90°,即∠OCP=90°,所以根据切线的判定定理得到PC为⊙O的切线.
解答: 解:(1)∵∠ACB=90°,AC=8cm,BC=6cm,
解:(1)∵∠ACB=90°,AC=8cm,BC=6cm,
∴AB=
=10cm,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠BAD=∠ABD=45°,
∴△ABD为等腰直角三角形,
∴AD=
AB=5
cm;
(2)直线PC与⊙O相切.理由如下:
连结OC,如图,
∵PE=PC,
∴∠PCE=∠PEC,
∵∠PCE=∠1+∠BCE=∠1+45°,∠PEC=∠2+∠ACE=∠2+45°,
∴∠2=∠1,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
而∠3+∠OCB=90°,
∴∠1+∠OCB=90°,即∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线.
 解:(1)∵∠ACB=90°,AC=8cm,BC=6cm,
解:(1)∵∠ACB=90°,AC=8cm,BC=6cm,∴AB=
| AC2+BC2 |
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠BAD=∠ABD=45°,
∴△ABD为等腰直角三角形,
∴AD=
| ||
| 2 |
| 2 |
(2)直线PC与⊙O相切.理由如下:
连结OC,如图,
∵PE=PC,
∴∠PCE=∠PEC,
∵∠PCE=∠1+∠BCE=∠1+45°,∠PEC=∠2+∠ACE=∠2+45°,
∴∠2=∠1,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
而∠3+∠OCB=90°,
∴∠1+∠OCB=90°,即∠OCP=90°,
∴OC⊥PC,
∴PC为⊙O的切线.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线;在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
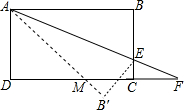 如图,在矩形ABCD中,AB=6cm,BC=3cm,点E是线段BC上的一个动点,连接AE并延长交DC延长线于点F,将△ABE沿直线AE翻折,点B落在B′处.线段AB′交CD于M点.当BE=2cm时,求DM.
如图,在矩形ABCD中,AB=6cm,BC=3cm,点E是线段BC上的一个动点,连接AE并延长交DC延长线于点F,将△ABE沿直线AE翻折,点B落在B′处.线段AB′交CD于M点.当BE=2cm时,求DM.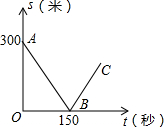 甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题:
甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题: △ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G.
△ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G. 如图,△ABC的中线AE,BD相交于点G,DF∥BC交AE于点F,求
如图,△ABC的中线AE,BD相交于点G,DF∥BC交AE于点F,求