题目内容
已知正比例函数y1=k1x和一次函数y2=k2x+b的图象交于点A(3,4),一次函数与y轴相交于点B,O为坐标原点,且△AOB是以OA为腰的等腰三角形.
(1)求正比例函数解析式;
(2)求一次函数解析式和△AOB面积.
(1)求正比例函数解析式;
(2)求一次函数解析式和△AOB面积.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)把A点坐标代入y1=k1x可计算出k1=
,从而得到正比例函数解析式;
(2)先利用勾股定理计算出AB=5,再分类讨论:当OB=OA时,则B点坐标为(0,5)或(0,-5),利用待定系数法求经过B(0,5)和A(3,4)的一次函数解析式,然后计算S△AOB;同样求经过点B(0,-5)和A(3,4)的一次函数解析式,计算S△AOB;当AB=AO时,B点坐标为(0,8),然后利用待定系数法求经过B(0,8)和A(3,4)的一次函数解析式为y2=-
x+8,再计算S△AOB.
| 4 |
| 3 |
(2)先利用勾股定理计算出AB=5,再分类讨论:当OB=OA时,则B点坐标为(0,5)或(0,-5),利用待定系数法求经过B(0,5)和A(3,4)的一次函数解析式,然后计算S△AOB;同样求经过点B(0,-5)和A(3,4)的一次函数解析式,计算S△AOB;当AB=AO时,B点坐标为(0,8),然后利用待定系数法求经过B(0,8)和A(3,4)的一次函数解析式为y2=-
| 4 |
| 3 |
解答:解:(1)把A(3,4)代入y1=k1x得3k1=4,解得k1=
,
所以正比例函数解析式为y1=
x;
(2)∵A(3,4),
∴OA=
=5,
当OB=OA时,B点坐标为(0,5)或(0,-5),
把B(0,5)和A(3,4)代入y2=k2x+b得
,解得
,此时一次函数解析式为y2=-
x+5,S△AOB=
×5×3=
;
把B(0,-5)和A(3,4)代入y2=k2x+b得
,解得
,此时一次函数解析式为y2=3x-5,S△AOB=
×5×3=
;
当AB=AO时,B点坐标为(0,8),
把B(0,8)和A(3,4)代入y2=k2x+b得
,解得
,此时一次函数解析式为y2=-
x+8,S△AOB=
×8×3=12.
| 4 |
| 3 |
所以正比例函数解析式为y1=
| 4 |
| 3 |
(2)∵A(3,4),
∴OA=
| 32+42 |
当OB=OA时,B点坐标为(0,5)或(0,-5),
把B(0,5)和A(3,4)代入y2=k2x+b得
|
|
| 1 |
| 3 |
| 1 |
| 2 |
| 15 |
| 2 |
把B(0,-5)和A(3,4)代入y2=k2x+b得
|
|
| 1 |
| 2 |
| 15 |
| 2 |
当AB=AO时,B点坐标为(0,8),
把B(0,8)和A(3,4)代入y2=k2x+b得
|
|
| 4 |
| 3 |
| 1 |
| 2 |
点评:本题要求利用图象求解各问题,要认真体会点的坐标,一次函数与一元一次方程组之间的内在联系.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
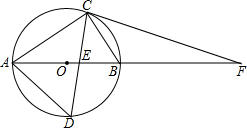 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,⊙O是△ABC的外接圆,∠ACB的平分线分别交⊙O、AB于点D、E,延长AB使PC=PE. 如图,一个边长为4cm的等边三角形ABC与⊙O等高,⊙O与BC相切于点C,⊙O与AC相交于点D,则阴影部分的面积为
如图,一个边长为4cm的等边三角形ABC与⊙O等高,⊙O与BC相切于点C,⊙O与AC相交于点D,则阴影部分的面积为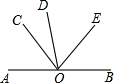 如图,已知A,O,B在一条直线上,OE平分∠BOD,∠COD=
如图,已知A,O,B在一条直线上,OE平分∠BOD,∠COD=
 A、B、C都在格点上,且每个小正方的边长都为1.已知AC=5,求B到直线AC的垂线段距离.
A、B、C都在格点上,且每个小正方的边长都为1.已知AC=5,求B到直线AC的垂线段距离. 如图,OM、ON、OP分别是∠AOB、∠BOC、∠AOC的平分线,则∠AOP与∠MON的大小上有何关系?请你写出你的推测,并简要说明理由.
如图,OM、ON、OP分别是∠AOB、∠BOC、∠AOC的平分线,则∠AOP与∠MON的大小上有何关系?请你写出你的推测,并简要说明理由. 如图是一个几何体的三视图,则这个几何体的侧面积是
如图是一个几何体的三视图,则这个几何体的侧面积是