题目内容

利用一面墙（墙的长度足够用），用30m长的篱笆，怎样围成一个面积为60㎡的矩形场地？设矩形场地的长（长与墙平行）为x，则可列方程为
 
．
考点：由实际问题抽象出一元二次方程
专题：几何图形问题
分析：欲求怎样围成一个面积为60m2的矩形场地，利用方程思想解决．先设矩形场地的长为xm，计算出矩形的面积得到一个关于x的方程，解之即得．
解答：解：设矩形场地的长为xm，
由题意列方程得 x×
30-x
2
=60，
整理得x2-30x+120=0，
故答案为：x2-30x+120=0．
点评：本题考查的是一元二次方程的应用，要会把实际问题的数量关系转化成一元二次方程的问题解决，难度一般．
练习册系列答案
相关题目
如图1，抛物线C1：y=x2+bx+c的顶点为A(1，-
13
4
)，与y轴的负半轴交于B点．
（1）求抛物线C1的解析式及B点的坐标；
（2）如图2，将抛物线C1向下平移与直线AB相交于C、D两点，若BC+AD=AB，求平移后的抛物线C2的解析式；
（3）如图3在（2）中，设抛物线C2与y轴交于G点，顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNG=90°，请你分析实数m的变化范围．
（1）计算：(
3
)0+
27
-4cos30°          
（2）化简：（1-3a）2-2（1-3a）．
有一种皮球是由40块黑白相间的牛皮缝制而成的（如图），黑皮可看作五边形，白皮可看作六边形，每块黑皮的周围都是白皮，而每块白皮有三条边和黑皮边在一起，则白皮有（　　）
A、16块B、20块
C、25块D、26块
周末，Lily和Joe去体育馆打羽毛球，比赛前，他俩决定用游戏的方式决定谁先开球，游戏规则是：两人同时伸出一只手的手指．
（1）求两人伸出的手指之和为6的概率．
（2）若两人伸出的手指之和为偶数，Lily先开球，否则，Joe先开球，你认为谁先开球的可能性大？为什么？
已知一元二次方程x2+mx+3=0配方后为（x+n）2=22，那么一元二次方程x2-mx-3=0配方后为（　　）
A、（x+5）2=28
B、（x+5）2=19或（x-5）2=19
C、（x-5）2=19
D、（x+5）2=28或（x-5）2=28
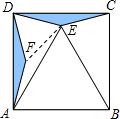已知：E是正方形ABCD内一点，且∠ECD=∠EDC=15°，求证：△ABE是等边三角形，小萍同学灵活运用全等变换，将△ECD进行旋转与翻折，使△ECD≌△FAD，巧妙地解答了此题．请按照小萍的思路，探究并解答下列问题：
（1）证明：△DEF是等边三角形；
（2）证明：△ECD≌△FAE；
（3）证明：△ABE是等边三角形．
下列运算正确的是（　　）
A、a3-a2=a
B、x6÷x2=x3
C、（x3）2=x6
D、a5•a2=a10
计算
1
3
5
÷
2
15
-(
3
+1)2=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网