题目内容
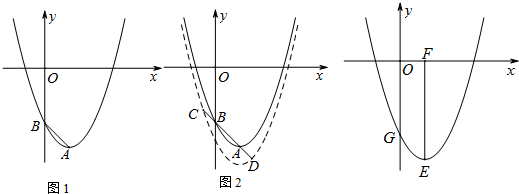
如图1,抛物线C1:y=x2+bx+c的顶点为A(1,-
),与y轴的负半轴交于B点.
(1)求抛物线C1的解析式及B点的坐标;
(2)如图2,将抛物线C1向下平移与直线AB相交于C、D两点,若BC+AD=AB,求平移后的抛物线C2的解析式;
(3)如图3在(2)中,设抛物线C2与y轴交于G点,顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNG=90°,请你分析实数m的变化范围.
| 13 |
| 4 |
(1)求抛物线C1的解析式及B点的坐标;
(2)如图2,将抛物线C1向下平移与直线AB相交于C、D两点,若BC+AD=AB,求平移后的抛物线C2的解析式;
(3)如图3在(2)中,设抛物线C2与y轴交于G点,顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNG=90°,请你分析实数m的变化范围.

考点:二次函数综合题
专题:综合题,压轴题
分析:(1)根据二次函数的顶点坐标为(-
,
),然后代入即可求出b和c的值,令x=0,求出此时的y,即是点B的纵坐标;
(2)过A、B两点分别作x轴、y轴的垂线,交于H点,过C、D两点分别作x轴、y轴的垂线,交于Q点,由(1)有直线AB的解析式为:y=-x-
,设C(m,-m-
),则D(m+2,-m-
),代入抛物线C2的解析式为y=x2-2x+t,求出即可;
(3)当M点在F点的右边时,作EM⊥GE交x轴于M点,当M点在F点的左边时,作GH⊥EF于H点,则△MNF∽△NGH,利用相似三角形的性质以及一元二次方程根的判别式得出m的取值范围.
| b |
| 2a |
| 4ac-b2 |
| 4a |
(2)过A、B两点分别作x轴、y轴的垂线,交于H点,过C、D两点分别作x轴、y轴的垂线,交于Q点,由(1)有直线AB的解析式为:y=-x-
| 9 |
| 4 |
| 9 |
| 4 |
| 17 |
| 4 |
(3)当M点在F点的右边时,作EM⊥GE交x轴于M点,当M点在F点的左边时,作GH⊥EF于H点,则△MNF∽△NGH,利用相似三角形的性质以及一元二次方程根的判别式得出m的取值范围.
解答:解:(1)由题意得:-
=1,
=-
,其中a=1,
解得:b=-2,c=-
,
∴抛物线C1的解析式:y=x2-2x-
;
令x=0,y=-
,
∴B点的坐标为(0,-
);
(2)过A、B两点分别作x轴、y轴的垂线,交于H点,过C、D两点分别作x轴、y轴的垂线,交于Q点,
∵BC+AD=AB,∴CD=2AB,
∵AH=BH=1,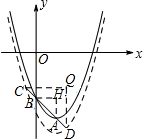 ∴CQ=DQ=2.
∴CQ=DQ=2.
设直线AB解析式为:y=kx+b,
由(1)中A,B两点坐标得出:
,
解得:
,
则直线AB的解析式为:y=-x-
,
设C(m,-m-
),则D(m+2,-m-
),
设抛物线C2的解析式为y=x2-2x+t,
∵C、D两点在抛物线C2上,
则有:
解得:
,
∴抛物线C2的解析式为y=x2-2x-3;
(3)由(2)有OF=1,FE=4,OG=3,∴∠GEF=45°,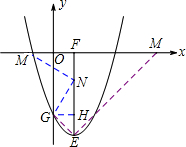
当M点在F点的右边时,
作EM⊥GE交x轴于M点,
则∠FEM=45°,
∴FM=EF=4,
∴OM=5,
∴m≤5;
当M点在F点的左边时,作GH⊥EF于H点,
∵∠MNG=90°,
则△MNF∽△NGH,
∴
=
,
设FN=n,则NH=3-n,
∴
=
,得:n2-3n-m+1=0,
∴△=(-3)2-4(-m+1)≥0,
解得:m≥-
.
∴m的变化范围是-
≤m≤5.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 13 |
| 4 |
解得:b=-2,c=-
| 9 |
| 4 |
∴抛物线C1的解析式:y=x2-2x-
| 9 |
| 4 |
令x=0,y=-
| 9 |
| 4 |
∴B点的坐标为(0,-
| 9 |
| 4 |
(2)过A、B两点分别作x轴、y轴的垂线,交于H点,过C、D两点分别作x轴、y轴的垂线,交于Q点,
∵BC+AD=AB,∴CD=2AB,
∵AH=BH=1,
 ∴CQ=DQ=2.
∴CQ=DQ=2.设直线AB解析式为:y=kx+b,
由(1)中A,B两点坐标得出:
|
解得:
|
则直线AB的解析式为:y=-x-
| 9 |
| 4 |
设C(m,-m-
| 9 |
| 4 |
| 17 |
| 4 |
设抛物线C2的解析式为y=x2-2x+t,
∵C、D两点在抛物线C2上,
则有:
|
解得:
|
∴抛物线C2的解析式为y=x2-2x-3;
(3)由(2)有OF=1,FE=4,OG=3,∴∠GEF=45°,

当M点在F点的右边时,
作EM⊥GE交x轴于M点,
则∠FEM=45°,
∴FM=EF=4,
∴OM=5,
∴m≤5;
当M点在F点的左边时,作GH⊥EF于H点,
∵∠MNG=90°,
则△MNF∽△NGH,
∴
| MF |
| NH |
| FN |
| GH |
设FN=n,则NH=3-n,
∴
| 1-m |
| 3-n |
| n |
| 1 |
∴△=(-3)2-4(-m+1)≥0,
解得:m≥-
| 5 |
| 4 |
∴m的变化范围是-
| 5 |
| 4 |
点评:本题考查了二次函数的综合运用以及相似三角形的判定与性质,根据已知结合图象进行分类讨论得出是解题关键.

练习册系列答案
相关题目
 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.若∠AOD=54°,则∠DEB的度数为
如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.若∠AOD=54°,则∠DEB的度数为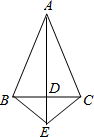 (1)如图,AB=AC,AE⊥BC于点D,求证:BE=CE.
(1)如图,AB=AC,AE⊥BC于点D,求证:BE=CE. 的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.
的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.