题目内容
2.当x≥5时,2(x-1)的值不小于8.分析 先根据题意得出关于x的不等式,再求出x的取值范围即可.
解答 解:∵2(x-1)的值不小于8,
∴2(x-1)≥8,解得x≥5.
故答案为:≥5.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
相关题目
10.八(2)班组织了一次环保知识竞赛,甲乙两队各5人的成绩如下表所示(10分制).
(1)指出甲队成绩的中位数;
(2)指出乙队成绩的众数;
(3)若计算出方差为:S${\;}_{甲}^{2}$=1.84,S${\;}_{乙}^{2}$=1.04,判断哪队的成绩更整齐?
| 甲 | 9 | 8 | 10 | 6 | 9 |
| 乙 | 8 | 7 | 8 | 9 | 10 |
(2)指出乙队成绩的众数;
(3)若计算出方差为:S${\;}_{甲}^{2}$=1.84,S${\;}_{乙}^{2}$=1.04,判断哪队的成绩更整齐?
17.若(x-1)2-9=0,则x=( )
| A. | ±9 | B. | ±3 | C. | 4或-2 | D. | -4或2 |
7.二次根式$\sqrt{2x-4}$中字母x的取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≤2 | D. | x<2 |
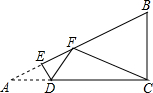 如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.
如图,有一直角三角形纸片ACB,∠A=30°,∠ACB=90°,BC=2,点D是AC边上一动点.过点D沿直线DE方向折叠三角形纸片,使点A落在射线AB上的点F处,当以点F、B、C为顶点的三角形为等腰三角形时,AD的长为$\frac{2\sqrt{3}}{3}$.

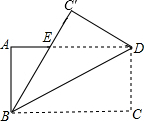 如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.
如图,将矩形ABCD沿对角线BD折叠,使点C与C′重合.若AB=3,则C′D的长为3.